题目内容
【题目】如图,已知A、B、C、D是平面直角坐标系中坐标轴上的点,且△AOB≌△COD,设直线AB的表达式为y1=ax+b,直线CD的表达式为y2=mx+n,则am= . 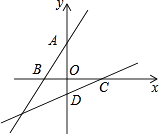
【答案】1
【解析】解:设点A的坐标为(0,y)、点B的坐标为(﹣x,0)(x、y均为正数), ∵△AOB≌△COD,
∴OC=OA,OD=OB,
结合图形可知点C的坐标为(y,0),点D的坐标为(0,﹣x).
将点A(0,y)、B(﹣x,0)代入y1=ax+b中,![]() ,
,
∴a= ![]() ;
;
将点C(y,0),D(0,﹣x)代入y2=mx+n,![]() ,m=
,m= ![]() .
.
∴am= ![]()
![]() =1.
=1.
所以答案是:1.
【考点精析】认真审题,首先需要了解全等三角形的性质(全等三角形的对应边相等; 全等三角形的对应角相等).

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目