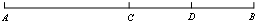题目内容
 如图,AB=12cm,M点是线段AB的中点,点C将线段MB分成MC:CB=1:2则线段AC的长度是
如图,AB=12cm,M点是线段AB的中点,点C将线段MB分成MC:CB=1:2则线段AC的长度是8
8
cm.分析:设MC=xcm,由MC:CB=1:2得到CB=2xcm,则MB=3x,根据M点是线段AB的中点,AB=12cm,得到AM=MB=
AB=
×12=3x,可求出x的值,又AC=AM+MC=4x,即可得到AC的长.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设MC=xcm,则CB=2xcm,
∴MB=3x,
∵M点是线段AB的中点,AB=12cm,
∴AM=MB=
AB=
×12=3x,
∴x=2,
而AC=AM+MC,
∴AC=3x+x=4x=4×2=8(cm).
故答案为8.
∴MB=3x,
∵M点是线段AB的中点,AB=12cm,
∴AM=MB=
| 1 |
| 2 |
| 1 |
| 2 |
∴x=2,
而AC=AM+MC,
∴AC=3x+x=4x=4×2=8(cm).
故答案为8.
点评:本题考查了两点间的距离:两点的连线段的长叫两点间的距离.也考查了方程思想的运用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目