题目内容
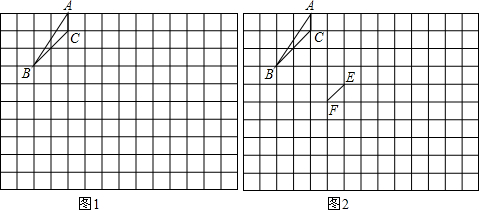
如图,边长为1的正方形格纸中,△ABC是一个格点三角形(在方格纸中,小正方形的顶点称格点,以格点连线为边的三角形叫做格点三角形).
(1)在图(1)的方格纸中,画出一个与△ABC相似但不全等的△A′B′C′;
(2)在图(2)中,以线段EF为边画格点三角形,其中能够与△ABC相似的有______个(不要证明)
(3)在图(2)的方格纸中,以线段EF为边,画出一个与△ABC相似的格点三角形______EFM,并证明.
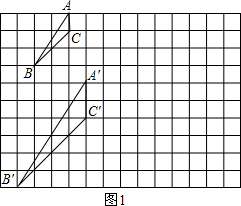
解:(1)图形正确(画全等不给分)
(2)4个,
分析,若三角形EFM要与△ABC相似,只能有一个角是135°,
若∠M为135°,则EF是最长边,不可能画出格点三角形,所以只能是∠FEM或∠EFM是135°,
所以FM是最长边或EM是最长边,∠FEM=135°时,
若EF是最短边时,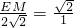 ,EM=4,只可以画出两个格点三角形.
,EM=4,只可以画出两个格点三角形.
(若EF是次长边时,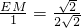 ,
,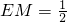 ,不可能画出格点三角形.)同理当∠EFM是135°时,FM=4.
,不可能画出格点三角形.)同理当∠EFM是135°时,FM=4.
又只可以画出两个格点三角形.所以共可以画出4个格点三角形.或根据对称性亦可知共可以画出4个格点三角形.
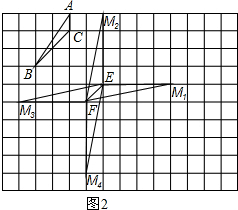
(3)画出一个格点三角形,
证明:∵△ABC的三边长是AC=1,BC=2 ,AB=
,AB= ,
,
所画的三角形EFM的三边分别是 ,4,
,4,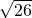 ,
,
∵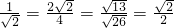 ,
,
∴两个三角形的三边对应成比例,
△ABC∽△EFM.
分析:(1)根据三边对应比值相等,画出即可;
(2)根据若三角形EFM要与△ABC相似,只能有一个角是135°,若∠M为135°,则EF是最长边,不可能画出格点三角形,所以只能是∠FEM或∠EFM是135°,得出即可;
(3)根据三角形各边长度得出两个三角形的三边对应成比例,即可证出△ABC∽△EFM.
点评:此题主要考查了相似三角形的判定以及相似三角形的性质和格点三角形的定义,根据相似三角形的性质得出符合要求的三角形是解决问题的关键.

(2)4个,
分析,若三角形EFM要与△ABC相似,只能有一个角是135°,
若∠M为135°,则EF是最长边,不可能画出格点三角形,所以只能是∠FEM或∠EFM是135°,
所以FM是最长边或EM是最长边,∠FEM=135°时,
若EF是最短边时,
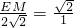 ,EM=4,只可以画出两个格点三角形.
,EM=4,只可以画出两个格点三角形.(若EF是次长边时,
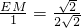 ,
,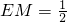 ,不可能画出格点三角形.)同理当∠EFM是135°时,FM=4.
,不可能画出格点三角形.)同理当∠EFM是135°时,FM=4.又只可以画出两个格点三角形.所以共可以画出4个格点三角形.或根据对称性亦可知共可以画出4个格点三角形.

(3)画出一个格点三角形,
证明:∵△ABC的三边长是AC=1,BC=2
 ,AB=
,AB= ,
,所画的三角形EFM的三边分别是
 ,4,
,4,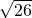 ,
,∵
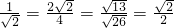 ,
,∴两个三角形的三边对应成比例,
△ABC∽△EFM.
分析:(1)根据三边对应比值相等,画出即可;
(2)根据若三角形EFM要与△ABC相似,只能有一个角是135°,若∠M为135°,则EF是最长边,不可能画出格点三角形,所以只能是∠FEM或∠EFM是135°,得出即可;
(3)根据三角形各边长度得出两个三角形的三边对应成比例,即可证出△ABC∽△EFM.
点评:此题主要考查了相似三角形的判定以及相似三角形的性质和格点三角形的定义,根据相似三角形的性质得出符合要求的三角形是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
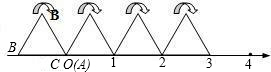
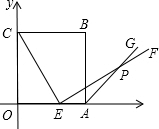 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.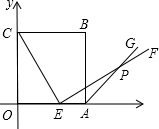 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.