题目内容
课本第五册第65页有一题:已知一元二次方程ax2-
| 2 |
| 2 |
小敏解得此题的正确答案“∠B=120°”后,思考以下问题,请你帮助解答.
(1)若在原题中,将方程改为ax2-
| 3 |
(2)若在原题中,将方程改为ax2-
| n |
分析:(1)因为∠B=120°,a=c,所以b=
a,代入原方程得△=5a2>0,故可根据一元二次方程根与系数的关系解答;
(2)同(1).
| 3 |
(2)同(1).
解答:解:(1)∵∠B=120°,a=c.
∴b=
a.
则原方程可化为ax2-3ax+a=0.
△=9a2-4a2=5a2>0.
又∵|x1-x2|=
=
.
∴|x1-x2|=
;
(2)若∠B=120°.
则b=
a代入原方程得ax2-
ax+c=0.
由一元二次方程根与系数的关系可得,x1+x2=
=
.
x1•x2=
=1.
故|x1-x2|=
=
=
.
∴b=
| 3 |
则原方程可化为ax2-3ax+a=0.
△=9a2-4a2=5a2>0.
又∵|x1-x2|=
| (x1+x2)2-4x1x2 |
|
∴|x1-x2|=
| 5 |
(2)若∠B=120°.
则b=
| 3 |
| 3n |
由一元二次方程根与系数的关系可得,x1+x2=
| ||
| a |
| 3n |
x1•x2=
| c |
| a |
故|x1-x2|=
| (x1+x2)2-4x1x2 |
(
|
| 3n-4 |
点评:解决本题的关键是根据一元二次方程根与系数的关系,求出方程的两根的和与两根的积,理解|x1-x2|=
这一等量关系.
| (x1+x2)2-4x1x2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 bx+c=0的两个根满足|x1-x2|=
bx+c=0的两个根满足|x1-x2|= bx+c=0,要得到∠B=120°,而条件“a=c”不变,那么应对条件中的|x1-x2|的值作怎样的改变并说明理由;
bx+c=0,要得到∠B=120°,而条件“a=c”不变,那么应对条件中的|x1-x2|的值作怎样的改变并说明理由; bx+c=0(n为正整数,n≥2),要得到∠B=120°,而条件“a=c”不变,那么条件中的|x1-x2|的值应改为多少?(不必说明理由)
bx+c=0(n为正整数,n≥2),要得到∠B=120°,而条件“a=c”不变,那么条件中的|x1-x2|的值应改为多少?(不必说明理由) bx+c=0的两个根满足|x1-x2|=
bx+c=0的两个根满足|x1-x2|=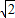 ,且a,b,c分别是△ABC的∠A,∠B,∠C的对边.若a=c,求∠B的度数.
,且a,b,c分别是△ABC的∠A,∠B,∠C的对边.若a=c,求∠B的度数.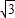 bx+c=0,要得到∠B=120°,而条件“a=c”不变,那么应对条件中的|x1-x2|的值作怎样的改变并说明理由;
bx+c=0,要得到∠B=120°,而条件“a=c”不变,那么应对条件中的|x1-x2|的值作怎样的改变并说明理由;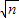 bx+c=0(n为正整数,n≥2),要得到∠B=120°,而条件“a=c”不变,那么条件中的|x1-x2|的值应改为多少?(不必说明理由)
bx+c=0(n为正整数,n≥2),要得到∠B=120°,而条件“a=c”不变,那么条件中的|x1-x2|的值应改为多少?(不必说明理由) bx+c=0的两个根满足|x1-x2|=
bx+c=0的两个根满足|x1-x2|=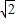 ,且a,b,c分别是△ABC的∠A,∠B,∠C的对边.若a=c,求∠B的度数.
,且a,b,c分别是△ABC的∠A,∠B,∠C的对边.若a=c,求∠B的度数.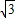 bx+c=0,要得到∠B=120°,而条件“a=c”不变,那么应对条件中的|x1-x2|的值作怎样的改变并说明理由;
bx+c=0,要得到∠B=120°,而条件“a=c”不变,那么应对条件中的|x1-x2|的值作怎样的改变并说明理由;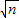 bx+c=0(n为正整数,n≥2),要得到∠B=120°,而条件“a=c”不变,那么条件中的|x1-x2|的值应改为多少?(不必说明理由)
bx+c=0(n为正整数,n≥2),要得到∠B=120°,而条件“a=c”不变,那么条件中的|x1-x2|的值应改为多少?(不必说明理由)