题目内容
某通信器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元.在销售过程中发现,年销售量y(万件)与销售单价x(元)之间存在着一次函数关系y=| 1 |
| 20k |
| k+1 |
| 1-k |
(1)求出这个函数关系式;
(2)试写出该公司销售该种产品的年获利z(万元)关于销售单价x(元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支).当销售单价x为何值时,年获利最大并求这个最大值;
(3)若公司希望该种产品一年的销售获利不低于40万元,借助(2)中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
分析:(1)弄清题意和题目中的数量关系,(2)根据题意列出不等式组或方程,(3)解答.
解答:解:(1)由
∴-1≤k≤1
∴k=1或k=-1(1分)
当k=1时,
>0,年销售量随售价x增大而增大,不合.
∴-1,y=-
x+b(2分)
把x=60,y=50000件=5万件代入,5=-
×60+b,b=8
∴y=-
x+8(3分)
(2)z=yx-40y-120=(-
x+8)(x-40)-120=-
x2+10x-440=-
(x-100)2+60(4分)
∴当x=100元时,年获利最大值为60万元.(5分)
(3)令z=40,得40=-
x2+10x-440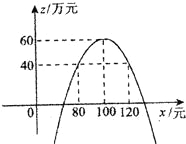
整理得x2-200x+9600=0(6分)
解得:x1=80,x2=120.(7分)
由图象可知,(画图并标上数据1分)要使年获利不低于40万元,销售单价应在80元到120元之间,(说明此点1分)又因为销售单价越低,销售量越大,所以要使销售量最大,又要使年获利不低于40万元,则销售单价应定为80元.(说明此点1分)(10分)
|
|
∴-1≤k≤1
∴k=1或k=-1(1分)
当k=1时,
| 1 |
| 20k |
∴-1,y=-
| 1 |
| 20 |
把x=60,y=50000件=5万件代入,5=-
| 1 |
| 20 |
∴y=-
| 1 |
| 20 |
(2)z=yx-40y-120=(-
| 1 |
| 20 |
| 1 |
| 20 |
| 1 |
| 20 |
∴当x=100元时,年获利最大值为60万元.(5分)
(3)令z=40,得40=-
| 1 |
| 20 |

整理得x2-200x+9600=0(6分)
解得:x1=80,x2=120.(7分)
由图象可知,(画图并标上数据1分)要使年获利不低于40万元,销售单价应在80元到120元之间,(说明此点1分)又因为销售单价越低,销售量越大,所以要使销售量最大,又要使年获利不低于40万元,则销售单价应定为80元.(说明此点1分)(10分)
点评:本题信息量较大,在考查提取、筛选信息,分析、解决实际问题等能力的同时,培养了同学们数形结合的思想.

练习册系列答案
相关题目
 ,其中整数k使式子
,其中整数k使式子 有意义.经测算,销售单价60元时,年销售量为50000件.
有意义.经测算,销售单价60元时,年销售量为50000件. ,其中整数k使式子
,其中整数k使式子 有意义.经测算,销售单价60元时,年销售量为50000件.
有意义.经测算,销售单价60元时,年销售量为50000件. ,其中整数k使式子
,其中整数k使式子 有意义.经测算,销售单价60元时,年销售量为50000件.
有意义.经测算,销售单价60元时,年销售量为50000件. ,其中整数k使式子
,其中整数k使式子 有意义.经测算,销售单价60元时,年销售量为50000件.
有意义.经测算,销售单价60元时,年销售量为50000件.