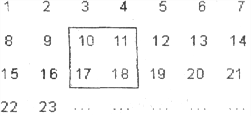
��Ŀ����
����Ŀ����ͼ����֪A��B�ֱ�Ϊ�����ϵ����㣬��A��ʾ�����ǩ�30����B��ʾ������50��
![]()
��1����д���߶�AB�е�M��ʾ�������� ����
��2������һֻ����P�ӵ�B��������ÿ��3����λ���ȵ��ٶ������������ƶ���ͬʱ��һֻ����Qǡ�ôӵ�A��������ÿ��2����λ���ȵ��ٶ������������ƶ�������ֻ�����������ϵĵ�C������
����A��B�����ľ��룻
������ֻ�����������ϵĵ�C����ʱ���õ�ʱ�䣻
�����C��Ӧ�����Ƕ��٣�
��3��������P�ӵ�B��������ÿ��3����λ���ȵ��ٶ������������˶���ͬʱ��һֻ����ǡ�ô�A���������ÿ��2����λ���ȵ��ٶ�������Ҳ�����˶�������ֻ�����������ϵ�D����������D���ʾ�����Ƕ��٣�
���𰸡���1��10����2����80����16�룻��2����3��-190.
��������
���ȼ����AB���ȣ��ٸ����е�ƽ���߶οɵõ�M��ʾ������
��A��B��ľ����������ʾ�������мӼ����㼴�ɵã�
����·�̳����ٶȼ��ɱ�ʾʱ�䣻
����50��ȥ����P������·�̼��ɵã�
��3������ֻ����t���������������ã�����A��������������ݵ�����ϵ�г����̣�Ȼ��ɼ�����˶�ʱ�䣬�ٸ���A���ʾ�����������ɵ�D���Ӧ����.
�⣺��1��AB=50+����30��=20
��AB�е�M��ʾ������10��
�ʴ�Ϊ��10
��2����A��B�����ľ���Ϊ��50������30��=80
����ֻ�����������ϵĵ�C����ʱ���õ�ʱ��Ϊ��80�£�3+2��=16���룩
�۵�C��Ӧ�����ǣ�50��16��3=2
��3������ֻ����t����������ɵ�: 2t+80=3t
��� t=80
�� D���ʾ�����ǣ�-( ![]() )-30=��190.
)-30=��190.

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ijУ���꼶��һ�ι㲥�ٱ����У�������ĸ���÷����±���
��װͳһ | �������� | ����ȷ | |
�ˣ�1���� | 80 | 84 | 87 |
�ˣ�2���� | 97 | 78 | 80 |
�ˣ�3���� | 90 | 78 | 85 |
(1) ��գ����ݱ����ṩ����Ϣ���ڷ�װͳһ���棬������÷ֵ�ƽ������_________���ڶ���ȷ�����������Ƶ���_________��
(2) �����װͳһ���������롢����ȷ�������水20%��30%��50%�ı����������ĵ÷֣���ͨ������˵���ĸ���ĵ÷����