题目内容
甲、乙两个不透明的纸盒中分别装有形状、大小和质地完全相同的四张和三张卡片.甲盒中的四张卡片上分别标有数字-1,0,1和2,乙盒中的三张卡片上分别标有数字-2,-1和1.小明从甲、乙两个纸盒中各随机抽取一张卡片,并分别将其卡片上的数字记为x,y,然后计算出S=x-y的值.请结合“树状图法”或“列表法”,求出当S<2时的概率.
解:画树状图得:

∴一共有12种情况,
S<2的有7种,
∴当S<2时的概率为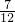 .
.
分析:根据概率的求法,找准两点:
①全部情况的总数;
②符合条件的情况数目;二者的比值就是其发生的概率.
使用树状图分析时,一定要做到不重不漏.
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

∴一共有12种情况,
S<2的有7种,
∴当S<2时的概率为
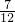 .
.分析:根据概率的求法,找准两点:
①全部情况的总数;
②符合条件的情况数目;二者的比值就是其发生的概率.
使用树状图分析时,一定要做到不重不漏.
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目



