题目内容
一个分母为7的最简真分数化成小数后,从小数点后第一位起,连续k位数字之和恰等于2005,则k=________或________.
(已知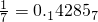 ,
,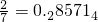 ,
,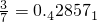 ,
,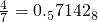 ,
,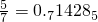 ,
,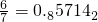 )
)
445 447
分析:认真观察题目中给出的已知条件可知,分母为7最简真分数化成小数后,按照1,4,2,8,5,7循环,而连续k位数字之和恰等于2005,然后用2005除以循环数字之和,即可得出答案.
解答:分母为7最简真分数化成小数后,按照1,4,2,8,5,7循环,
k位数字之和恰等于2005,2005÷(1+4+2+8+5+7)=74余7,
所以K=74×6+1=445或74×6+3=447.
故答案为:445或447.
点评:此题主要考查学生对数字有规律变化的理解和掌握,解答此题的关键是明确分母为7最简真分数化成小数后,按照1,4,2,8,5,7循环,而连续k位数字之和恰等于2005.此题有一定拔高难度,属于难题.
分析:认真观察题目中给出的已知条件可知,分母为7最简真分数化成小数后,按照1,4,2,8,5,7循环,而连续k位数字之和恰等于2005,然后用2005除以循环数字之和,即可得出答案.
解答:分母为7最简真分数化成小数后,按照1,4,2,8,5,7循环,
k位数字之和恰等于2005,2005÷(1+4+2+8+5+7)=74余7,
所以K=74×6+1=445或74×6+3=447.
故答案为:445或447.
点评:此题主要考查学生对数字有规律变化的理解和掌握,解答此题的关键是明确分母为7最简真分数化成小数后,按照1,4,2,8,5,7循环,而连续k位数字之和恰等于2005.此题有一定拔高难度,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目