题目内容
【题目】如图，AB∥CD，∠BED=61°，∠ABE的平分线与∠CDE的平分线交于点F，则∠DFB=（ ）
A. 149° B. 149.5° C. 150° D. 150.5°
【答案】B
【解析】
过点E作EG∥AB，根据平行线的性质可得“∠ABE+∠BEG=180°，∠GED+∠EDC=180°”，根据角的计算以及角平分线的定义可得“∠FBE+∠EDF=
∠ABE+∠CDE）”，再依据四边形内角和为360°结合角的计算即可得出结论．
如图，过点E作EG∥AB，
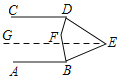
∵AB∥CD，
∴AB∥CD∥GE，
∴∠ABE+∠BEG=180°，∠GED+∠EDC=180°，
∴∠ABE+∠CDE+∠BED=360°；
又∵∠BED=61°，
∴∠ABE+∠CDE=299°．
∵∠ABE和∠CDE的平分线相交于F，
∴∠FBE+∠EDF=（∠ABE+∠CDE）=149.5°，
∵四边形的BFDE的内角和为360°，
∴∠BFD=360°-149.5°-61°=149.5°．
故选B．
练习册系列答案
相关题目
