题目内容
已知,二次函数y=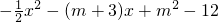 的图象与x轴相交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,图象与y轴交于点C,OB=2OA;
的图象与x轴相交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,图象与y轴交于点C,OB=2OA;
(1)求二次函数的解析式;
(2)在x轴上,点A的左侧,求一点E,使△ECO与△CAO相似,并说明直线EC经过(1)中二次函数图象的顶点D;
(3)过(2)中的点E的直线y=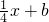 与(1)中的抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M′、N′,点P为线段MN上一点,点P的横坐标为t,过点P作平行于y轴的直线交(1)中所求抛物线于点Q,是否存在t值,使S梯形MM'N'N:S△QMN=35:12?若存在,求出满足条件的t值;若不存在,请说明理由.
与(1)中的抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M′、N′,点P为线段MN上一点,点P的横坐标为t,过点P作平行于y轴的直线交(1)中所求抛物线于点Q,是否存在t值,使S梯形MM'N'N:S△QMN=35:12?若存在,求出满足条件的t值;若不存在,请说明理由.
解:(1)∵二次函数y=- x2-(m+3)x+m2-12的图象与x轴相交于A(x1,0)、B(x2,0)两点,
x2-(m+3)x+m2-12的图象与x轴相交于A(x1,0)、B(x2,0)两点,
∴x1+x2=-2(m+3),x1x2=-2(m2-12).
又∵x1<0,x2>0,OB=2OA,
∴x2=-2x1.
整理得:m2+8m+16=0,
解得m1=m2=-4.
∴二次函数的解析式为:y=- x2+x+4.
x2+x+4.
(2)∵二次函数的解析式为:y=- x2+x+4,
x2+x+4,
∴点A(-2,0)、B(4,0)、C(0,4).
设点E(x,0),则OE=-x.
∵∠COA=∠EOC=90°,
要使△ECO∽△CAO,
只有 .
.
∴ ,
,
∴x=-8.
∴当点E坐标为(-8,0),△ECO与△CAO相似.
设直线EC解析式为:y=k′x+b′,
将点E、点C的坐标代入得: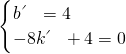 ,
,
解得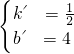 ,
,
∴直线EC的解析式为:y= x+4.
x+4.
∵抛物线顶点D(1, ),
),
分别将点D的坐标代入解析式的左右式,得到左式=右式.
∴直线EC经过(1)中抛物线的顶点D.
(3)存在t值,使S梯形MM'N'N:S△QMN=35:12.
∵直线y= x+b过点E(-8,0),
x+b过点E(-8,0),
∴0= ×(-8)+b,
×(-8)+b,
∴b=2.
∴y= x+2.
x+2.
∴x=4(y-2)
∵直线y= x+2与(1)中的二次函数y=-
x+2与(1)中的二次函数y=- x2+x+4相交于M、N两点,
x2+x+4相交于M、N两点,
∴y=- +4(y-2)+4,整理得8y2-35y+36=0.
+4(y-2)+4,整理得8y2-35y+36=0.
设M(xm,ym),N(xn,yn),
∴MM′=ym,NN′=yn.
∴ym,yn是方程8y2-35y+36=0的两个实数根,
∴ym+yn=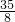 .
.
∴S梯形MM'N'N= (ym+yn)(xn-xm).∵点P在直线y=
(ym+yn)(xn-xm).∵点P在直线y= x+2上,点Q在(1)中的抛物线上,
x+2上,点Q在(1)中的抛物线上,
∴点P(t, t+2),点Q(t,-
t+2),点Q(t,- t2+t+4).
t2+t+4).
∴PQ=- t2+t+4-
t2+t+4- t-2=-
t-2=- t2+
t2+ t+2,
t+2,
分别过M、N作直线PQ的垂线,垂足为点G、H,
则GM=t-xm,NH=xn-t.
∴S△QMN=S△QMP+S△QNP= =
= PQ•(xn-xm)=
PQ•(xn-xm)= (-
(- t2+
t2+ t+2)(xn-xm).
t+2)(xn-xm).
∵S梯形MM'N'N:S△QMN=35:12,
∴ ,
,
∴ .
.
整理得:2t2-3t-2=0,
解得:t1=- ,t2=2.
,t2=2.
∴当t=- 或t=2时,S梯形MM'N'N:S△QMN=35:12.
或t=2时,S梯形MM'N'N:S△QMN=35:12.
分析:(1)由二次函数y=- x2-(m+3)x+m2-12的图象与x轴相交于A(x1,0)、B(x2,0)两点,根据根与系数的关系与OB=2OA,即可求得m的值,则可得二次函数的解析式;
x2-(m+3)x+m2-12的图象与x轴相交于A(x1,0)、B(x2,0)两点,根据根与系数的关系与OB=2OA,即可求得m的值,则可得二次函数的解析式;
(2)由二次函数的解析式为:y=- x2+x+4,求得A,B,C的坐标,设点E(x,0),则OE=-x,根据相似三角形的判定方法即可求得点E的坐标,然后设直线EC解析式为:y=k′x+b′,由待定系数法即可求得直线EC的解析式,又由抛物线顶点D(1,
x2+x+4,求得A,B,C的坐标,设点E(x,0),则OE=-x,根据相似三角形的判定方法即可求得点E的坐标,然后设直线EC解析式为:y=k′x+b′,由待定系数法即可求得直线EC的解析式,又由抛物线顶点D(1, ),分别将点D的坐标代入解析式的左右式,即可得直线EC经过(1)中抛物线的顶点D;
),分别将点D的坐标代入解析式的左右式,即可得直线EC经过(1)中抛物线的顶点D;
(3)由直线y= x+2与(1)中的二次函数y=-
x+2与(1)中的二次函数y=- x2+x+4相交于M、N两点,设M(xm,ym),N(xn,yn),可得MM′=ym,NN′=yn.又由ym,yn是方程8y2-35y+36=0的两个实数根,求得ym+yn的值,继而求得点P(t,
x2+x+4相交于M、N两点,设M(xm,ym),N(xn,yn),可得MM′=ym,NN′=yn.又由ym,yn是方程8y2-35y+36=0的两个实数根,求得ym+yn的值,继而求得点P(t, t+2),点Q(t,-
t+2),点Q(t,- t2+t+4).又由S△QMN=S△QMP+S△QNP与S梯形MM'N'N:S△QMN=35:12,则可求得当t=-
t2+t+4).又由S△QMN=S△QMP+S△QNP与S梯形MM'N'N:S△QMN=35:12,则可求得当t=- 或t=2时,S梯形MM'N'N:S△QMN=35:12.
或t=2时,S梯形MM'N'N:S△QMN=35:12.
点评:此题考查了待定系数法求函数的解析式,根与系数的关系点与函数的关系以及三角形的面积问题等知识.此题综合性很强,难度很大,解题的关键是方程思想与数形结合思想的应用.
 x2-(m+3)x+m2-12的图象与x轴相交于A(x1,0)、B(x2,0)两点,
x2-(m+3)x+m2-12的图象与x轴相交于A(x1,0)、B(x2,0)两点,∴x1+x2=-2(m+3),x1x2=-2(m2-12).
又∵x1<0,x2>0,OB=2OA,
∴x2=-2x1.
整理得:m2+8m+16=0,
解得m1=m2=-4.
∴二次函数的解析式为:y=-
 x2+x+4.
x2+x+4.(2)∵二次函数的解析式为:y=-
 x2+x+4,
x2+x+4,∴点A(-2,0)、B(4,0)、C(0,4).
设点E(x,0),则OE=-x.
∵∠COA=∠EOC=90°,
要使△ECO∽△CAO,
只有
 .
.∴
 ,
,∴x=-8.
∴当点E坐标为(-8,0),△ECO与△CAO相似.
设直线EC解析式为:y=k′x+b′,
将点E、点C的坐标代入得:
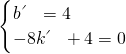 ,
,解得
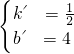 ,
,∴直线EC的解析式为:y=
 x+4.
x+4.∵抛物线顶点D(1,
 ),
),分别将点D的坐标代入解析式的左右式,得到左式=右式.
∴直线EC经过(1)中抛物线的顶点D.

(3)存在t值,使S梯形MM'N'N:S△QMN=35:12.
∵直线y=
 x+b过点E(-8,0),
x+b过点E(-8,0),∴0=
 ×(-8)+b,
×(-8)+b,∴b=2.
∴y=
 x+2.
x+2.∴x=4(y-2)
∵直线y=
 x+2与(1)中的二次函数y=-
x+2与(1)中的二次函数y=- x2+x+4相交于M、N两点,
x2+x+4相交于M、N两点,∴y=-
 +4(y-2)+4,整理得8y2-35y+36=0.
+4(y-2)+4,整理得8y2-35y+36=0.设M(xm,ym),N(xn,yn),
∴MM′=ym,NN′=yn.
∴ym,yn是方程8y2-35y+36=0的两个实数根,
∴ym+yn=
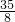 .
.∴S梯形MM'N'N=
 (ym+yn)(xn-xm).∵点P在直线y=
(ym+yn)(xn-xm).∵点P在直线y= x+2上,点Q在(1)中的抛物线上,
x+2上,点Q在(1)中的抛物线上,∴点P(t,
 t+2),点Q(t,-
t+2),点Q(t,- t2+t+4).
t2+t+4).∴PQ=-
 t2+t+4-
t2+t+4- t-2=-
t-2=- t2+
t2+ t+2,
t+2,分别过M、N作直线PQ的垂线,垂足为点G、H,
则GM=t-xm,NH=xn-t.
∴S△QMN=S△QMP+S△QNP=
 =
= PQ•(xn-xm)=
PQ•(xn-xm)= (-
(- t2+
t2+ t+2)(xn-xm).
t+2)(xn-xm).∵S梯形MM'N'N:S△QMN=35:12,
∴
 ,
,∴
 .
.整理得:2t2-3t-2=0,
解得:t1=-
 ,t2=2.
,t2=2.∴当t=-
 或t=2时,S梯形MM'N'N:S△QMN=35:12.
或t=2时,S梯形MM'N'N:S△QMN=35:12.分析:(1)由二次函数y=-
 x2-(m+3)x+m2-12的图象与x轴相交于A(x1,0)、B(x2,0)两点,根据根与系数的关系与OB=2OA,即可求得m的值,则可得二次函数的解析式;
x2-(m+3)x+m2-12的图象与x轴相交于A(x1,0)、B(x2,0)两点,根据根与系数的关系与OB=2OA,即可求得m的值,则可得二次函数的解析式;(2)由二次函数的解析式为:y=-
 x2+x+4,求得A,B,C的坐标,设点E(x,0),则OE=-x,根据相似三角形的判定方法即可求得点E的坐标,然后设直线EC解析式为:y=k′x+b′,由待定系数法即可求得直线EC的解析式,又由抛物线顶点D(1,
x2+x+4,求得A,B,C的坐标,设点E(x,0),则OE=-x,根据相似三角形的判定方法即可求得点E的坐标,然后设直线EC解析式为:y=k′x+b′,由待定系数法即可求得直线EC的解析式,又由抛物线顶点D(1, ),分别将点D的坐标代入解析式的左右式,即可得直线EC经过(1)中抛物线的顶点D;
),分别将点D的坐标代入解析式的左右式,即可得直线EC经过(1)中抛物线的顶点D;(3)由直线y=
 x+2与(1)中的二次函数y=-
x+2与(1)中的二次函数y=- x2+x+4相交于M、N两点,设M(xm,ym),N(xn,yn),可得MM′=ym,NN′=yn.又由ym,yn是方程8y2-35y+36=0的两个实数根,求得ym+yn的值,继而求得点P(t,
x2+x+4相交于M、N两点,设M(xm,ym),N(xn,yn),可得MM′=ym,NN′=yn.又由ym,yn是方程8y2-35y+36=0的两个实数根,求得ym+yn的值,继而求得点P(t, t+2),点Q(t,-
t+2),点Q(t,- t2+t+4).又由S△QMN=S△QMP+S△QNP与S梯形MM'N'N:S△QMN=35:12,则可求得当t=-
t2+t+4).又由S△QMN=S△QMP+S△QNP与S梯形MM'N'N:S△QMN=35:12,则可求得当t=- 或t=2时,S梯形MM'N'N:S△QMN=35:12.
或t=2时,S梯形MM'N'N:S△QMN=35:12.点评:此题考查了待定系数法求函数的解析式,根与系数的关系点与函数的关系以及三角形的面积问题等知识.此题综合性很强,难度很大,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
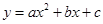
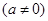 中的
中的 满足下表:
满足下表:
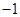
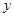

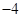
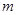
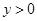 时的
时的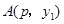 ,
, 两点都在该函数图象上,且
两点都在该函数图象上,且 ,试比较
,试比较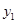 与
与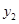 的大小.
的大小.  的图象与x轴相交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,图象与y轴交于点C,OB=2OA;
的图象与x轴相交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,图象与y轴交于点C,OB=2OA; 与(1)中的抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M′、N′,点P为线段MN上一点,点P的横坐标为t,过点P作平行于y轴的直线交(1)中所求抛物线于点Q,是否存在t值,使S梯形MM'N'N:S△QMN=35:12?若存在,求出满足条件的t值;若不存在,请说明理由.
与(1)中的抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M′、N′,点P为线段MN上一点,点P的横坐标为t,过点P作平行于y轴的直线交(1)中所求抛物线于点Q,是否存在t值,使S梯形MM'N'N:S△QMN=35:12?若存在,求出满足条件的t值;若不存在,请说明理由.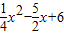 的图象与x轴从左到右的两个交点依次为A、B,与y轴交点为C;
的图象与x轴从左到右的两个交点依次为A、B,与y轴交点为C; 中的x、y满足下表:
中的x、y满足下表:
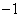
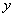
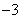

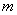
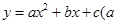 ≠0的图像经过点(3,5)、(2,8)、(0,8).
≠0的图像经过点(3,5)、(2,8)、(0,8).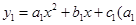 ≠0,
≠0,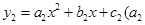 ≠0,且满足
≠0,且满足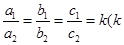 ≠0,1,则我们称抛物线
≠0,1,则我们称抛物线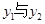 互为“友好抛物线”,请写出当
互为“友好抛物线”,请写出当 时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.
时第(1)小题中的抛物线的友好抛物线,并求出这友好抛物线的顶点坐标.