题目内容
(2010•顺义区二模)在平面直角坐标系xOy中,抛物线y=x2+bx+c经过A(2,0)、B(4,0)两点,直线 交y轴于点C,且过点D(8,m).
交y轴于点C,且过点D(8,m).(1)求抛物线的解析式;
(2)在x轴上找一点P,使CP+DP的值最小,求出点P的坐标;
(3)将抛物线y=x2+bx+c左右平移,记平移后点A的对应点为A′,点B的对应点为B′,当四边形A′B′DC的周长最小时,求抛物线的解析式及此时四边形A′B′DC周长的最小值.

【答案】分析:(1)将A、B点的坐标代入抛物线的解析式中即可求出待定系数的值;
(2)根据已知直线的解析式可求出C点的坐标,作C关于x轴的对称点C′,连接C′D,与x轴的交点即为所求的P点,可先求出直线C′D的解析式,进而求出P点的坐标;
(3)由于A′B′、CD都是定长,若四边形A′B′DC的周长最小,那么A′C+B′D就最短,此时C′A′应该平行于B′D,很显然抛物线应该向左平移,可将D向左平移2个单位(即AB的长)得到D′,那么C′D′与x轴的交点即为所求的A′,可先求出直线C′D′的解析式,然后再求得A′的坐标,也就能得到B′的坐标,用待定系数法即可求得平移后抛物线的解析式;此时四边形A′B′DC的最小周长为:C′D′+AB+CD.
解答:解:(1)由于抛物线经过A(2,0),B(4,0),则有:
y=(x-2)(x-4)=x2-6x+8;
(2)易知:C(0,2),D(8,6);
作C关于x轴的对称点C′(0,-2),连接C′D,点P即为直线C′D与x轴的交点;
设直线C′D的解析式为:y=kx-2,则有:
8k-2=6,k=1;
∴直线C′D的解析式为y=x-2;则P点坐标为:P(2,0);
(3) 当抛物线向右平移时,A′C+B′D>AC+BD,显然不存在符合条件的抛物线;
当抛物线向右平移时,A′C+B′D>AC+BD,显然不存在符合条件的抛物线;
当抛物线向左平移时,设平移后A′(x,0),B′(x+2,0);
若平移后四边形A′B′DC的周长最小,那么A′C+B′D就应该最小;
将D向左平移2个单位,得:D′(6,6);
若四边形A′B′DC的周长最小,那么C′、A′、D′就应该在同一直线上,
设直线C′D′的解析式为:y=k′x-2,则有:6k′-2=6,k′= ;
;
∴直线C′D′的解析式为y= x-2,
x-2,
则A′( ,0),B′(
,0),B′( ,0);
,0);
∴此时抛物线的解析式为:y=(x- )(x-
)(x- )=x2-5x+
)=x2-5x+ ;
;
此时四边形A′B′DC的周长为:A′B′+A′C+B′D+CD=AB+CD+C′D′=2+4 +10=12+4
+10=12+4 .
.
点评:此题主要考查了一次函数与二次函数解析式的确定、函数图象交点坐标的求法等知识;能够确定四边形A′B′DC的周长最小时A′的具体位置是解答此题的关键.
(2)根据已知直线的解析式可求出C点的坐标,作C关于x轴的对称点C′,连接C′D,与x轴的交点即为所求的P点,可先求出直线C′D的解析式,进而求出P点的坐标;
(3)由于A′B′、CD都是定长,若四边形A′B′DC的周长最小,那么A′C+B′D就最短,此时C′A′应该平行于B′D,很显然抛物线应该向左平移,可将D向左平移2个单位(即AB的长)得到D′,那么C′D′与x轴的交点即为所求的A′,可先求出直线C′D′的解析式,然后再求得A′的坐标,也就能得到B′的坐标,用待定系数法即可求得平移后抛物线的解析式;此时四边形A′B′DC的最小周长为:C′D′+AB+CD.
解答:解:(1)由于抛物线经过A(2,0),B(4,0),则有:
y=(x-2)(x-4)=x2-6x+8;
(2)易知:C(0,2),D(8,6);
作C关于x轴的对称点C′(0,-2),连接C′D,点P即为直线C′D与x轴的交点;
设直线C′D的解析式为:y=kx-2,则有:
8k-2=6,k=1;
∴直线C′D的解析式为y=x-2;则P点坐标为:P(2,0);
(3)
 当抛物线向右平移时,A′C+B′D>AC+BD,显然不存在符合条件的抛物线;
当抛物线向右平移时,A′C+B′D>AC+BD,显然不存在符合条件的抛物线;当抛物线向左平移时,设平移后A′(x,0),B′(x+2,0);
若平移后四边形A′B′DC的周长最小,那么A′C+B′D就应该最小;
将D向左平移2个单位,得:D′(6,6);
若四边形A′B′DC的周长最小,那么C′、A′、D′就应该在同一直线上,
设直线C′D′的解析式为:y=k′x-2,则有:6k′-2=6,k′=
 ;
;∴直线C′D′的解析式为y=
 x-2,
x-2,则A′(
 ,0),B′(
,0),B′( ,0);
,0);∴此时抛物线的解析式为:y=(x-
 )(x-
)(x- )=x2-5x+
)=x2-5x+ ;
;此时四边形A′B′DC的周长为:A′B′+A′C+B′D+CD=AB+CD+C′D′=2+4
 +10=12+4
+10=12+4 .
.点评:此题主要考查了一次函数与二次函数解析式的确定、函数图象交点坐标的求法等知识;能够确定四边形A′B′DC的周长最小时A′的具体位置是解答此题的关键.

练习册系列答案
相关题目
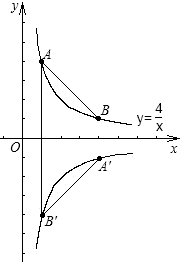 (2010•顺义区二模)在平面直角坐标系xOy中,A、B为反比例函数
(2010•顺义区二模)在平面直角坐标系xOy中,A、B为反比例函数 (x>0)的图象上两点,A点的横坐标与B点的纵坐标均为1,将
(x>0)的图象上两点,A点的横坐标与B点的纵坐标均为1,将 (x>0)的图象绕原点O顺时针旋转90°,A点的对应点为A′,B点的对应点为B′.
(x>0)的图象绕原点O顺时针旋转90°,A点的对应点为A′,B点的对应点为B′.
