题目内容
(1)如图,把一个等腰直角△ABC沿斜边上的高BD(裁剪线)剪一刀,从这个三角形中裁下一部分,与剩下部分拼成一个四边形A′BCD(见示意图A).
①猜一猜,四边形A′BCD一定是________形.
②试一试,按上述裁剪方法,请你拼一个与图A形状不同的四边形,并在图B中画出示意图.
(2)在等腰直角三角形△ABC中,请你找出与(1)不同的裁剪线,把分割成的两部分拼成一个特殊的四边形,请你在图C中画出你拼得的特殊的四边形的示意图.

解:(1)①根据题意得:A′C=BD,∠BDC=∠A′CD,
∴A′C∥BD,
∴四边形A′BCD一定是平行四边形;
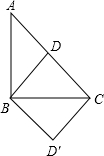 ②将AB边与BC边重合,
②将AB边与BC边重合,
∵BD是等腰直角三角形ABC斜边上的高,
∴AD=CD=BD= AC,
AC,
∴BD=CD=CD′=BD′,
∴四边形BDCD′是菱形,
∵∠BDC=90°,
∴四边形BDCD′是正方形;
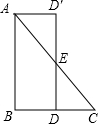 (2)分别取AC于BC的中点,沿DE剪下△DEC,
(2)分别取AC于BC的中点,沿DE剪下△DEC,
∴DE∥AB,
∵△ABC是直角三角形,
∴∠B=90°,
∴∠AD′E=∠EDC=∠EDB=∠B=90°,
∴四边形AD′DB是矩形.
分析:(1)根据已知可得:A′C=BD,∠BDC=∠A′CD,即可证得四边形A′BCD是平行四边形;
(2)根据已知,可证得:BD=CD=CD′=BD′,∠BDC=90°,则可得:四边形BDCD′是正方形;
(3)分别取AC于BC的中点,沿DE剪下△DEC,
即可证得:∠AD′E=∠EDC=∠EDB=∠B=90°,则可得:四边形AD′DB是矩形.
点评:此题考查了平行四边形,矩形,正方形的判定以及等腰直角三角形的性质.考查了学生的动手能力,注意数形结合思想的应用.
∴A′C∥BD,
∴四边形A′BCD一定是平行四边形;
 ②将AB边与BC边重合,
②将AB边与BC边重合,∵BD是等腰直角三角形ABC斜边上的高,
∴AD=CD=BD=
 AC,
AC,∴BD=CD=CD′=BD′,
∴四边形BDCD′是菱形,
∵∠BDC=90°,
∴四边形BDCD′是正方形;
 (2)分别取AC于BC的中点,沿DE剪下△DEC,
(2)分别取AC于BC的中点,沿DE剪下△DEC,∴DE∥AB,
∵△ABC是直角三角形,
∴∠B=90°,
∴∠AD′E=∠EDC=∠EDB=∠B=90°,
∴四边形AD′DB是矩形.
分析:(1)根据已知可得:A′C=BD,∠BDC=∠A′CD,即可证得四边形A′BCD是平行四边形;
(2)根据已知,可证得:BD=CD=CD′=BD′,∠BDC=90°,则可得:四边形BDCD′是正方形;
(3)分别取AC于BC的中点,沿DE剪下△DEC,
即可证得:∠AD′E=∠EDC=∠EDB=∠B=90°,则可得:四边形AD′DB是矩形.
点评:此题考查了平行四边形,矩形,正方形的判定以及等腰直角三角形的性质.考查了学生的动手能力,注意数形结合思想的应用.

练习册系列答案
相关题目
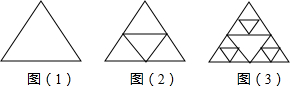
 20、如图,把一个等边三角形进行分割,第一步从图(1)到图(2),一个三角形分为4个三角形;第二步从图(2)到图(3),将4个三角形分为13个三角形.按这个规律分割下去,第3步分割完成后共有
20、如图,把一个等边三角形进行分割,第一步从图(1)到图(2),一个三角形分为4个三角形;第二步从图(2)到图(3),将4个三角形分为13个三角形.按这个规律分割下去,第3步分割完成后共有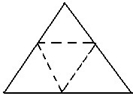 15、如图,把一个等边三角形(正三角形)三边的中点用虚线连接起来,沿着虚线折叠起来,得到的几何体是( )
15、如图,把一个等边三角形(正三角形)三边的中点用虚线连接起来,沿着虚线折叠起来,得到的几何体是( ) 如图,把一个等边三角形的顶点放置在正六边形的中心O点,请你借助这个等边三角形的角,以角为工具等分正六边形的面积,等分的情况分别为
如图,把一个等边三角形的顶点放置在正六边形的中心O点,请你借助这个等边三角形的角,以角为工具等分正六边形的面积,等分的情况分别为