题目内容
(2013•荆门模拟)关于x的二次函数y=a(x+1)(x-m),其图象的对称轴在y轴的右侧,则实数a、m应满足( )
分析:先令a(x+1)(x-m)=0求出x的值即可得出二次函数与x轴的交点坐标,再根据抛物线的对称轴在y轴的右侧即可得到关于m的不等式,求出m的取值范围即可.
解答:解:∵a(x+1)(x-m)=0,则x=-1或x=m,且a≠0,
∴二次函数y=a(x+1)(x-m)的图象与x轴的交点为(-1,0)、(m,0),
∴二次函数的对称轴x=
,
∵函数图象的对称轴在y轴的右侧,
∴
>0,
解得:m>1,
故选:D.
∴二次函数y=a(x+1)(x-m)的图象与x轴的交点为(-1,0)、(m,0),
∴二次函数的对称轴x=
| -1+m |
| 2 |
∵函数图象的对称轴在y轴的右侧,
∴
| -1+m |
| 2 |
解得:m>1,
故选:D.
点评:本题考查的是抛物线与x轴的交点问题,先根据函数的解析式得出二次函数的图象与x轴的交点是解答此题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
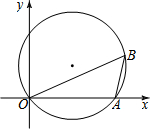 (2013•荆门模拟)如图,已知点A(8,0),sin∠ABO=
(2013•荆门模拟)如图,已知点A(8,0),sin∠ABO=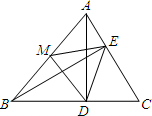 (2013•荆门模拟)已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连结ME、MD、ED.设AB=4,∠DBE=30°.则△EDM的面积为( )
(2013•荆门模拟)已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连结ME、MD、ED.设AB=4,∠DBE=30°.则△EDM的面积为( )