题目内容
【题目】如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于F,连接AD. 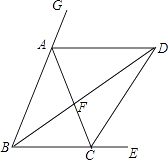
(1)求证:∠BDC= ![]() ∠BAC;
∠BAC;
(2)若AB=AC,请判断△ABD的形状,并证明你的结论;
(3)在(2)的条件下,若AF=BF,求∠EBA的大小.
【答案】
(1)解:∵BD、CD分别平分∠EBA、∠ECA,BD交AC于F,
∴∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠ACE,∠BAC+∠ABC=∠ACE,
∠ACE,∠BAC+∠ABC=∠ACE,
∴∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠BAC+
∠BAC+ ![]() ∠ABC,
∠ABC,
∴∠BDC= ![]() ∠BAC
∠BAC
(2)解:△ABD为等腰三角形,证明如下:
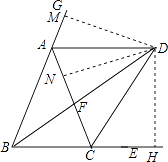
作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H
∵BD、CD分别平分∠EBA、∠ECA,
∴DM=DH,DN=DH,
∴DM=DN,
∴AD平分∠CAG,即∠GAD=∠CAD,
∵∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,
∴∠GAD+∠CAD=∠ABC+∠ACB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠GAD=∠ABC,
∴AD∥BC,
∴∠ADB=∠DBC,
又∵∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD,
∴△ABD为等腰三角形
(3)解:∵AF=BF,
∴∠BAF=∠ABF= ![]() ∠ABC,
∠ABC,
∵∠BAF+∠ABC+∠ACB=180°,∠ABC=∠ACB,
∴ ![]() ∠ABC=180°,
∠ABC=180°,
∴∠ABC=72°.
【解析】(1)根据角平分线的定义得到∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠ACE,∠BAC+∠ABC=∠ACE,于是得到∠BDC+
∠ACE,∠BAC+∠ABC=∠ACE,于是得到∠BDC+ ![]() ∠ABC=
∠ABC= ![]() ∠BAC+
∠BAC+ ![]() ∠ABC,等量代换即可得到结论;(2)作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H根据角平分线的性质得到DM=DH,DN=DH,等量代换得到DM=DN,根据三角形的内角和得到∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,推出∠GAD+∠CAD=∠ABC+∠ACB,由等腰三角形的性质得到∠ABC=∠ACB,等量代换得到∠GAD=∠ABC,推出AD∥BC,由平行线的性质得到∠ADB=∠DBC,证得∠ABD=∠ADB,即可得到结论;(3)根据等腰三角形的性质得到∠BAF=∠ABF=
∠ABC,等量代换即可得到结论;(2)作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H根据角平分线的性质得到DM=DH,DN=DH,等量代换得到DM=DN,根据三角形的内角和得到∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,推出∠GAD+∠CAD=∠ABC+∠ACB,由等腰三角形的性质得到∠ABC=∠ACB,等量代换得到∠GAD=∠ABC,推出AD∥BC,由平行线的性质得到∠ADB=∠DBC,证得∠ABD=∠ADB,即可得到结论;(3)根据等腰三角形的性质得到∠BAF=∠ABF= ![]() ∠ABC,根据三角形的内角和即可得到结论.
∠ABC,根据三角形的内角和即可得到结论.