题目内容
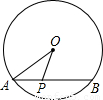
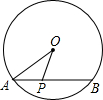 如图,半径为5cm,弦AB=8cm,点P是弦AB上的一个动点,(不与A、B两点重合),则OP可能为________cm.(写出一个符合条件的长度即可).
如图,半径为5cm,弦AB=8cm,点P是弦AB上的一个动点,(不与A、B两点重合),则OP可能为________cm.(写出一个符合条件的长度即可).
4(答案不唯一)
分析:过O作OC⊥AB,则此时P与C重合时OP最小,根据垂径定理求出AC=BC=4cm,由勾股定理求出OC=3cm,得出OP的范围是3cm≤OP<5cm,即可得出答案.
解答: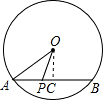
解:过O作OC⊥AB,则此时P与C重合时OP最小,
∵OC⊥AB,
∴根据垂径定理得:AC=BC=4cm,
在Rt△OAC中,AC=4cm,OA=5cm,由勾股定理得:OC=3cm,
故OP的范围是3cm≤OP<5cm,
只要在范围内取任何数都符合,如4.
故答案为:4.
点评:本题考查了勾股定理,垂径定理,垂线段最短等知识点,主要考查学生分析问题和解决问题的能力,关键是求出OP的范围,是一道开放型的题目,答案不唯一.
分析:过O作OC⊥AB,则此时P与C重合时OP最小,根据垂径定理求出AC=BC=4cm,由勾股定理求出OC=3cm,得出OP的范围是3cm≤OP<5cm,即可得出答案.
解答:

解:过O作OC⊥AB,则此时P与C重合时OP最小,
∵OC⊥AB,
∴根据垂径定理得:AC=BC=4cm,
在Rt△OAC中,AC=4cm,OA=5cm,由勾股定理得:OC=3cm,
故OP的范围是3cm≤OP<5cm,
只要在范围内取任何数都符合,如4.
故答案为:4.
点评:本题考查了勾股定理,垂径定理,垂线段最短等知识点,主要考查学生分析问题和解决问题的能力,关键是求出OP的范围,是一道开放型的题目,答案不唯一.

练习册系列答案
相关题目
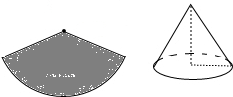 如图,半径为5cm、圆心角为144°的一个扇形纸片,制作成一个圆锥形玩具纸帽(接缝处不重叠),那么这个圆锥的高为
如图,半径为5cm、圆心角为144°的一个扇形纸片,制作成一个圆锥形玩具纸帽(接缝处不重叠),那么这个圆锥的高为 如图,半径为5cm的⊙O,OC⊥AB,弦AB长为8cm,则弦心距OC长为
如图,半径为5cm的⊙O,OC⊥AB,弦AB长为8cm,则弦心距OC长为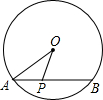 (2012•镇赉县模拟)如图,半径为5cm,弦AB=8cm,点P是弦AB上的一个动点,(不与A、B两点重合),则OP可能为
(2012•镇赉县模拟)如图,半径为5cm,弦AB=8cm,点P是弦AB上的一个动点,(不与A、B两点重合),则OP可能为 如图,半径为5cm的⊙O中,弦AB=8cm,则圆心O到线段AB中点C的距离为
如图,半径为5cm的⊙O中,弦AB=8cm,则圆心O到线段AB中点C的距离为