题目内容
(2005•四川)如图,一次函数y=ax+b的图象与反比例函数y= 的图象交于A、B两点,与x轴交于点C,与y轴交于点D.已知OA=
的图象交于A、B两点,与x轴交于点C,与y轴交于点D.已知OA= ,tan∠AOC=
,tan∠AOC= ,点B的坐标为(
,点B的坐标为( ,m).
,m).(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.

【答案】分析:(1)根据tan∠AOC= ,且OA=
,且OA=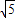 ,结合勾股定理可以求得点A的坐标,进一步代入y=
,结合勾股定理可以求得点A的坐标,进一步代入y= 中,得到反比例函数的解析式;然后根据反比例函数的解析式得到点B的坐标,再根据待定系数法求一次函数解析式;
中,得到反比例函数的解析式;然后根据反比例函数的解析式得到点B的坐标,再根据待定系数法求一次函数解析式;
(2)三角形AOB的面积可利用,求和的方法即等于S△AOC+S△COB来求.
解答: 解:(1)过点A作AH⊥x于点H.
解:(1)过点A作AH⊥x于点H.
在RT△AHO中,tan∠AOH= =
= ,
,
所以OH=2AH.
又AH2+HO2=OA2,且OA= ,
,
所以AH=1,OH=2,
即点A(-2,1).
代入y= 得
得
k=-2.
∴反比例函数的解析式为y=-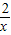 .
.
又因为点B的坐标为( ,m),
,m),
代入解得m=-4.
∴B( ,-4).
,-4).
把A(-2,1)B( ,-4)代入y=ax+b,得
,-4)代入y=ax+b,得
 ,
,
∴a=-2,b=-3.
∴一次函数的解析式为y=-2x-3.
(2)在y=-2x-3中,当y=0时,x=- .
.
即C( ,0).
,0).
∴S△AOB=S△AOC+S△COB= (1+4)×
(1+4)× =
=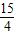 .
.
点评:此题综合考查了解直角三角形、待定系数法、和函数的基本知识,难易程度适中.
 ,且OA=
,且OA=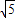 ,结合勾股定理可以求得点A的坐标,进一步代入y=
,结合勾股定理可以求得点A的坐标,进一步代入y= 中,得到反比例函数的解析式;然后根据反比例函数的解析式得到点B的坐标,再根据待定系数法求一次函数解析式;
中,得到反比例函数的解析式;然后根据反比例函数的解析式得到点B的坐标,再根据待定系数法求一次函数解析式;(2)三角形AOB的面积可利用,求和的方法即等于S△AOC+S△COB来求.
解答:
 解:(1)过点A作AH⊥x于点H.
解:(1)过点A作AH⊥x于点H.在RT△AHO中,tan∠AOH=
 =
= ,
,所以OH=2AH.
又AH2+HO2=OA2,且OA=
 ,
,所以AH=1,OH=2,
即点A(-2,1).
代入y=
 得
得k=-2.
∴反比例函数的解析式为y=-
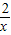 .
.又因为点B的坐标为(
 ,m),
,m),代入解得m=-4.
∴B(
 ,-4).
,-4).把A(-2,1)B(
 ,-4)代入y=ax+b,得
,-4)代入y=ax+b,得 ,
,∴a=-2,b=-3.
∴一次函数的解析式为y=-2x-3.
(2)在y=-2x-3中,当y=0时,x=-
 .
.即C(
 ,0).
,0).∴S△AOB=S△AOC+S△COB=
 (1+4)×
(1+4)× =
=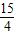 .
.点评:此题综合考查了解直角三角形、待定系数法、和函数的基本知识,难易程度适中.

练习册系列答案
相关题目
 (2005•四川)如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面与右面所标注代数式的值相等,则x的值为
(2005•四川)如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面与右面所标注代数式的值相等,则x的值为 的图象交于A、B两点,与x轴交于点C,与y轴交于点D.已知OA=
的图象交于A、B两点,与x轴交于点C,与y轴交于点D.已知OA= ,tan∠AOC=
,tan∠AOC= ,点B的坐标为(
,点B的坐标为( ,m).
,m).


 .
.