题目内容
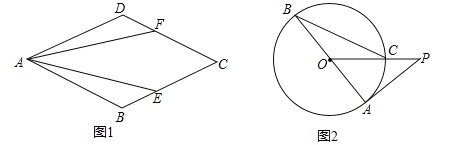
【题目】(1)如图1,在菱形ABCD中,CE=CF,求证:AE=AF.
(2)如图2,AB是⊙O的直径,PA与⊙O相切于点A,OP与⊙O相交于点C,连接CB,∠OPA=40°,求∠ABC的度数.
【答案】(1)证明见解析;(2)25°.
【解析】
试题分析:(1)根据菱形的性质,利用SAS判定△ABE≌△ADF,从而求得AE=AF;
(2)利用切线的性质和直角三角形的两个锐角互余的性质得到圆心角∠PAO的度数,然后利用圆周角定理来求∠ABC的度数.
试题解析:(1)∵四边形ABCD是菱形,∴AB=BC=CD=AD,∠B=∠D,∵CE=CF,∴BE=DF,在△ABE与△ADF中,∵AB=AD,∠B=∠D,BE=DF,∴△ABE≌△ADF,∴AE=AF;
(2)∵AB是⊙O的直径,直线PA与⊙O相切于点A,∴∠PAO=90°.
又∵∠OPA=40°,∴∠POA=50°,∴∠ABC=![]() ∠POA=25°.
∠POA=25°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目