题目内容
如图,在△ABC中,AB=AC=a,∠BAC=18°,动点P、Q分别在直线BC上运动,且始终保持∠PAQ=99°.设BP=x,CQ=y,则y与x之间的函数关系用图象大致可以表示为( )

A. | B. | C. | D. |

∵AB=AC=a,∠BAC=18°,
∴∠ABC=∠ACB=
(180°-18°)=81°,
∴∠ABC=∠APB+∠PAB=81°,
∵∠PAQ=99°,∠BAC=18°,
∴∠PAB+∠QAC=99°-18°=81°,
∴∠APB=∠QAC,
同理可得∠PAB=∠AQC,
∴△APB∽△QAC,
∴
=
,
即
=
,
整理得,y=
,
∵x、y都是边的长度,是正数,
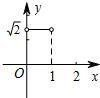
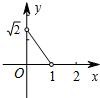
∴y与x之间的函数关系用图象表示是反比例函数在第一象限内的部分,
纵观各选项,只有A符合.
故选A.
∴∠ABC=∠ACB=
| 1 |
| 2 |
∴∠ABC=∠APB+∠PAB=81°,
∵∠PAQ=99°,∠BAC=18°,
∴∠PAB+∠QAC=99°-18°=81°,
∴∠APB=∠QAC,
同理可得∠PAB=∠AQC,
∴△APB∽△QAC,
∴
| BP |
| AC |
| AB |
| CQ |
即
| x |
| a |
| a |
| y |
整理得,y=
| a2 |
| x |
∵x、y都是边的长度,是正数,
∴y与x之间的函数关系用图象表示是反比例函数在第一象限内的部分,
纵观各选项,只有A符合.
故选A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目










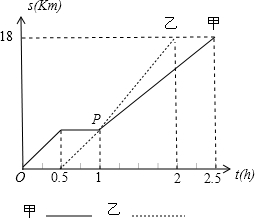 地的距离为S(km)和行驶时间t(h)之间的函数关系的图象如图所示,根据图中提供的信息,回答下列问题
地的距离为S(km)和行驶时间t(h)之间的函数关系的图象如图所示,根据图中提供的信息,回答下列问题