题目内容
求证:不论k取何值,关于x的方程x2-(2k+1)x+2(2k-1)=0总有实数根.
考点:根的判别式
专题:证明题,判别式法
分析:求出根的判别式,通过配方,得到完全平方式,从而判断出该式为非负数,即方程有实数根.
解答:解:∵△=[-(2k+1)]2-4×2(2k-1)=4k2-12k+9=4(k-
)2+6,
又∵不论k取何实数,总有(k-
)2≥0,
∴4(k-
)2+6≥6,即△>0,
∴不论k取何实数,方程都有实数根.
| 3 |
| 2 |
又∵不论k取何实数,总有(k-
| 3 |
| 2 |
∴4(k-
| 3 |
| 2 |
∴不论k取何实数,方程都有实数根.
点评:本题考查一元二次方程根的判别式,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
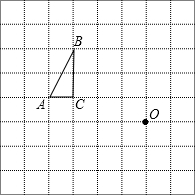 如图,每个小方格都是边长为1个单位长度的小正方形.
如图,每个小方格都是边长为1个单位长度的小正方形.