题目内容
(2013•下城区二模)已知矩形ABCD的边AB=4,AD=3,现将矩形ABCD如图放在直线l上,且沿着l向右作无滑动地翻滚,当它翻滚到位置A1B1C1D1时,计算:
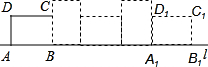
(1)顶点A所经过的路线长为
(2)点A经过的路线与直线l所围成的面积为
π+12
π+12.
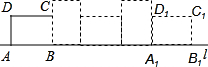
(1)顶点A所经过的路线长为
6π
6π
;(2)点A经过的路线与直线l所围成的面积为
| 25 |
| 2 |
| 25 |
| 2 |
分析:(1)根据图形的滚动路线得出顶点A所经过的路线长为3段扇形弧长进而求出即可;
(2)根据图形得出点A经过的路线与直线l所围成的面积为S扇形ABA′+S△A′BM+S扇形A′MF+S△MFN+S扇形FNA1求出即可.
(2)根据图形得出点A经过的路线与直线l所围成的面积为S扇形ABA′+S△A′BM+S扇形A′MF+S△MFN+S扇形FNA1求出即可.
解答: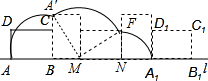 解:(1)如图所示:
解:(1)如图所示:
∵AB=4,AD=3,
∴A′M=
=5,
顶点A所经过的路线长为:
+
+
=6π;
(2)点A经过的路线与直线l所围成的面积为:
S扇形ABA′+S△A′BM+S扇形A′MF+S△MFN+S扇形FNA1
=
+
×4×3+
+
×4×3+
,
=
π+12.
故答案为:6π;
π+12.
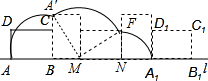 解:(1)如图所示:
解:(1)如图所示:∵AB=4,AD=3,
∴A′M=
| 42+32 |
顶点A所经过的路线长为:
| 90π×4 |
| 180 |
| 90×5π |
| 180 |
| 90×π×3 |
| 180 |
(2)点A经过的路线与直线l所围成的面积为:
S扇形ABA′+S△A′BM+S扇形A′MF+S△MFN+S扇形FNA1
=
| 90π×42 |
| 360 |
| 1 |
| 2 |
| 90π×52 |
| 360 |
| 1 |
| 2 |
| 90π×32 |
| 360 |
=
| 25 |
| 2 |
故答案为:6π;
| 25 |
| 2 |
点评:此题主要考查了图形的旋转以及扇形弧长公式和扇形面积公式应用,根据已知得出滚动路线是解题关键.

练习册系列答案
相关题目