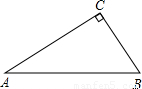
题目内容
某校把一块形状近似于直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,BC=60米,∠A=36度.(1)若入口E在边AB上,且与A、B等距离,请你在图中画出入口E到C点的最短路线,并求出最短路线CE的长.(保留整数)
(2)若线段CD是一条水渠,并且D点在边AB上,已知水渠造价为50元/米,水渠路线应如何设计
 才能使造价最低,请你画出水渠路线,并求出最低造价.
才能使造价最低,请你画出水渠路线,并求出最低造价.
分析:(1)E与A、B等距离应是AB的中点,CE的最短距离应是线段CE的长度,它等于AB的一半.利用∠A是正弦值即可求得AB长.
(2)点C到AB的最短距离应是点C到AB的垂线段的长度,利用∠B的正弦值即可求得CD长.
(2)点C到AB的最短距离应是点C到AB的垂线段的长度,利用∠B的正弦值即可求得CD长.
解答: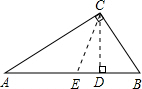 解:(1)最短路线如图所示:
解:(1)最短路线如图所示:
CE为Rt△ABC斜边上的中线
在Rt△ABC中,∠A=36°,BC=60米,
AB=
=
≈102(米)
CE=
AB=51(米)
(2)若要水渠造价最低,则水渠应与AB垂直,如图所示CD⊥AB
在Rt△BCD中,∠B=54°,BC=60米CD=BC•sin54°=60×0.809=48.54
造价:50×CD=2427元.
 解:(1)最短路线如图所示:
解:(1)最短路线如图所示:CE为Rt△ABC斜边上的中线
在Rt△ABC中,∠A=36°,BC=60米,
AB=
| BC |
| sin36° |
| 60 |
| 0.5878 |
CE=
| 1 |
| 2 |
(2)若要水渠造价最低,则水渠应与AB垂直,如图所示CD⊥AB
在Rt△BCD中,∠B=54°,BC=60米CD=BC•sin54°=60×0.809=48.54
造价:50×CD=2427元.
点评:本题考查锐角三角函数的运用;点到直线的最短距离应是这点到这条直线的垂线段的长度;应尽量使用题中已知的线段求解.

练习册系列答案
相关题目
 才能使造价最低,请你画出水渠路线,并求出最低造价.
才能使造价最低,请你画出水渠路线,并求出最低造价.