题目内容
(2004•深圳)等腰梯形ABCD中,如图1,AB∥CD,AD=BC,延长AB到E,使BE=CD,连接CE.(1)求证:CE=CA;
(2)上述条件下,如图2,若AF⊥CE于点F,且AF平分∠DAE,
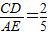 ,求sin∠CAF的值.
,求sin∠CAF的值.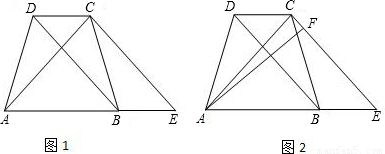
【答案】分析:(1)根据等腰梯形的性质可得出AC=BD,而CD BE,因此四边形CEBD是平行四边形,CE=BD,因此可得出CE=CA;
BE,因此四边形CEBD是平行四边形,CE=BD,因此可得出CE=CA;
(2)要求∠CAF的正弦值,就要知道,CF和AC的比例关系.由于BD∥CE,AF⊥CE,那么AF⊥BD,而AF平分∠DAB,因此AF垂直平分BD,如果设AF,BD交于O点,那么BO= BD=
BD= AC=
AC= CE.根据CD:AE=2:5,即BE:AE=2:5,可得出AB:AE=3:5,有BO∥CE,得出BO:EF=AB:AE,也就求出了BF何CE的比例关系,便可得出CF和EC的比例关系,由于CE=AC,因此也就得出了CF和AC的比例关系即可得出∠CAF的正弦值.
CE.根据CD:AE=2:5,即BE:AE=2:5,可得出AB:AE=3:5,有BO∥CE,得出BO:EF=AB:AE,也就求出了BF何CE的比例关系,便可得出CF和EC的比例关系,由于CE=AC,因此也就得出了CF和AC的比例关系即可得出∠CAF的正弦值.
解答:(1)证明:∵四边形ABCD是等腰梯形
∴AC=BD,CD∥BE,
∵CD=BE,
∴四边形DBEC是平行四边形
∴CE=BD,
∴CE=CA;
(2)解:∵CD=BE,且 ,
,
∴ =
=
∵AF⊥EC,BD∥EC
∴AF⊥BD,设垂足为O
∵AF平分∠DAB
∴AF垂直平分BD,即BO= BD=
BD= AC=
AC= CE
CE
∵BO∥CE
∴ =
=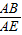 =
= ,即
,即 =
=
∴EF= CE
CE
∴CF= CE=
CE= AC
AC
∴sin∠CAF=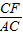 =
= .
.
点评:本题主要考查了等腰梯形的性质,相似三角形的性质等知识点的应用,本题中通过AF垂直平分BD得出BO= BD,进而求出EF和CE的关系是解题的关键.
BD,进而求出EF和CE的关系是解题的关键.
 BE,因此四边形CEBD是平行四边形,CE=BD,因此可得出CE=CA;
BE,因此四边形CEBD是平行四边形,CE=BD,因此可得出CE=CA;(2)要求∠CAF的正弦值,就要知道,CF和AC的比例关系.由于BD∥CE,AF⊥CE,那么AF⊥BD,而AF平分∠DAB,因此AF垂直平分BD,如果设AF,BD交于O点,那么BO=
 BD=
BD= AC=
AC= CE.根据CD:AE=2:5,即BE:AE=2:5,可得出AB:AE=3:5,有BO∥CE,得出BO:EF=AB:AE,也就求出了BF何CE的比例关系,便可得出CF和EC的比例关系,由于CE=AC,因此也就得出了CF和AC的比例关系即可得出∠CAF的正弦值.
CE.根据CD:AE=2:5,即BE:AE=2:5,可得出AB:AE=3:5,有BO∥CE,得出BO:EF=AB:AE,也就求出了BF何CE的比例关系,便可得出CF和EC的比例关系,由于CE=AC,因此也就得出了CF和AC的比例关系即可得出∠CAF的正弦值.解答:(1)证明:∵四边形ABCD是等腰梯形
∴AC=BD,CD∥BE,
∵CD=BE,
∴四边形DBEC是平行四边形
∴CE=BD,
∴CE=CA;
(2)解:∵CD=BE,且
 ,
,∴
 =
=
∵AF⊥EC,BD∥EC
∴AF⊥BD,设垂足为O
∵AF平分∠DAB
∴AF垂直平分BD,即BO=
 BD=
BD= AC=
AC= CE
CE∵BO∥CE
∴
 =
=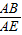 =
= ,即
,即 =
=
∴EF=
 CE
CE∴CF=
 CE=
CE= AC
AC∴sin∠CAF=
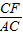 =
= .
.点评:本题主要考查了等腰梯形的性质,相似三角形的性质等知识点的应用,本题中通过AF垂直平分BD得出BO=
 BD,进而求出EF和CE的关系是解题的关键.
BD,进而求出EF和CE的关系是解题的关键. 
练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
 ,求sin∠CAF的值.
,求sin∠CAF的值.
 ,求sin∠CAF的值.
,求sin∠CAF的值.