题目内容
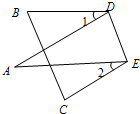
6、如图，将纸片△ABC沿着DE折叠压平，且∠1+∠2=72°，则∠A=
36°
．分析：由折叠及邻补角的性质可知，∠1=180°-2∠ADE，∠2=180°-2∠AED，两式相加，结合已知可求∠ADE+∠AED的度数，在△ADE中，由内角和定理可求∠A的度数．
解答：解：根据折叠及邻补角的性质，得
∠1=180°-2∠ADE，∠2=180°-2∠AED，
∴∠1+∠2=360°-2（∠ADE+∠AED），
把∠1+∠2=72°代入，得
∠ADE+∠AED=144°，
∴在△ADE中，由内角和定理，得
∠A=180°-（∠ADE+∠AED）=36°．
故答案为：36°．
∠1=180°-2∠ADE，∠2=180°-2∠AED，
∴∠1+∠2=360°-2（∠ADE+∠AED），
把∠1+∠2=72°代入，得
∠ADE+∠AED=144°，
∴在△ADE中，由内角和定理，得
∠A=180°-（∠ADE+∠AED）=36°．
故答案为：36°．
点评：本题考查了折叠的性质，邻补角的性质，三角形内角和定理，关键是把∠1+∠2看作整体，对角的和进行转化．
练习册系列答案
相关题目
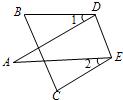7、如图，将纸片△ABC沿着DE折叠压平，且∠1+∠2=72°，则∠A=（ ）
5、如图，将纸片△ABC沿DE折叠，点A落在A′处，∠l+∠2=150°，则∠A=
24、如图，将纸片△ABC沿DE折叠，点A落在点P处，已知∠1+∠2=124°，求∠A的度数．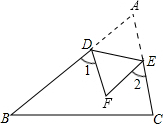
如图：将纸片△ABC沿DE折叠，点A落在点F处，已知∠1+∠2=100°，则∠A=