题目内容
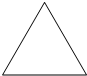 如图,正三角形外接圆的半径为2,那么这个正三角形的边长为
如图,正三角形外接圆的半径为2,那么这个正三角形的边长为2
| 3 |
2
.| 3 |
分析:连接OA,并作OD⊥AB于D,可求得AD=OA•cos30°=32,则AB=3.
解答: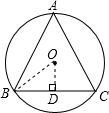 解:连接OA,并作OD⊥AB于D,则:
解:连接OA,并作OD⊥AB于D,则:
∠OAD=30°,
OA=2,
∴OD=1,
∴BD=
=
,
∴CB=2
.
故答案为2
.
 解:连接OA,并作OD⊥AB于D,则:
解:连接OA,并作OD⊥AB于D,则:∠OAD=30°,
OA=2,
∴OD=1,
∴BD=
| OB2-OD2 |
| 3 |
∴CB=2
| 3 |
故答案为2
| 3 |
点评:此题主要考查由外接圆的半径求内接等边三角形的边长.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 法是否合理?若不合理,请给出正n边形“接近度”的一个合理定义.
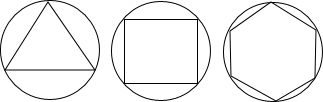
法是否合理?若不合理,请给出正n边形“接近度”的一个合理定义.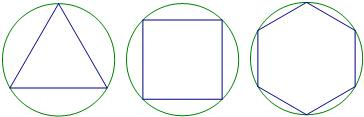
 法是否合理?若不合理,请给出正n边形“接近度”的一个合理定义.
法是否合理?若不合理,请给出正n边形“接近度”的一个合理定义.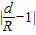 .分别计算n=3,n=6时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?
.分别计算n=3,n=6时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?