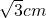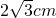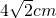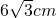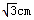题目内容
菱形的一个内角等于60°,较短对角线长等于2cm,则菱形较长对角线长等于( )
A、
| ||
B、2
| ||
C、4
| ||
D、6
|
分析:先证明出△ABD是等边三角形,可知∠OAD=30°,继而可求出AO的长,然后求出AC的长.
解答:解:如图,连接AC,则AC⊥BD,
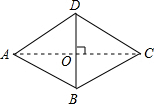
∵四边形ABCD是菱形,
∴AB=AD,
∵∠A=60°,
∴△ABD是等边三角形,∠OAD=30°,
∵菱形较短的对角线长是2cm,即BD=2cm
∴AO=
cm,AC=2
cm.
故选B.

∵四边形ABCD是菱形,
∴AB=AD,
∵∠A=60°,
∴△ABD是等边三角形,∠OAD=30°,
∵菱形较短的对角线长是2cm,即BD=2cm
∴AO=
| 3 |
| 3 |
故选B.
点评:此题考查了菱形的性质,难度适中,熟练掌握菱形的性质是关键.

练习册系列答案
相关题目
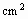 .
.