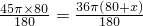题目内容
如图,六位朋友均匀的围坐在圆桌旁聚会.圆桌的半径为80cm,每人离桌边10cm,有后来两位客人,每人向后挪动了相同距离并左右调整位置,使8个人都坐下,每相邻两人之间的距离与原来相邻两人之间的距离(即在圆周上两人之间的圆弧的长)相等.设每人向后挪动的距离为xcm.则根据题意,可列方程为:( )
A.

B.

C.2π(80+10)×8=2π(80+x)×10
D.2π(80-x)×10=2π(80+x)×8
【答案】分析:首先理解题意找出题中存在的等量关系:坐6个人时两人之间的距离=坐8个人时两人之间的距离,根据等量关系列方程即可.
解答:解:设每人向后挪动的距离为xcm,应首先明确弧长公式:l=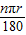 .
.
六位朋友每相邻两人之间的弧长所对的圆心角度数为60°,半径为(80+10)cm,即l=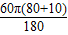 ;
;
八位朋友每相邻两人之间的弧长所对的圆心角度数为45°,半径为80+10+x,即l=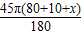 .
.
根据距离相等可列方程为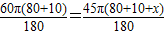 ,
,
故选A.
点评:此题应重点注意每相邻两人之间的距离指的是弧长.
解答:解:设每人向后挪动的距离为xcm,应首先明确弧长公式:l=
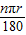 .
.六位朋友每相邻两人之间的弧长所对的圆心角度数为60°,半径为(80+10)cm,即l=
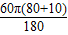 ;
;八位朋友每相邻两人之间的弧长所对的圆心角度数为45°,半径为80+10+x,即l=
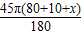 .
.根据距离相等可列方程为
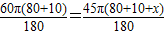 ,
,故选A.
点评:此题应重点注意每相邻两人之间的距离指的是弧长.

练习册系列答案
相关题目
 如图,六位朋友均匀的围坐在圆桌旁聚会.圆桌的半径为80cm,每人离桌边10cm,有后来两位客人,每人向后挪动了相同距离并左右调整位置,使8个人都坐下,每相邻两人之间的距离与原来相邻两人之间的距离(即在圆周上两人之间的圆弧的长)相等.设每人向后挪动的距离为xcm.则根据题意,可列方程为:( )
如图,六位朋友均匀的围坐在圆桌旁聚会.圆桌的半径为80cm,每人离桌边10cm,有后来两位客人,每人向后挪动了相同距离并左右调整位置,使8个人都坐下,每相邻两人之间的距离与原来相邻两人之间的距离(即在圆周上两人之间的圆弧的长)相等.设每人向后挪动的距离为xcm.则根据题意,可列方程为:( )A、
| ||||
B、
| ||||
| C、2π(80+10)×8=2π(80+x)×10 | ||||
| D、2π(80-x)×10=2π(80+x)×8 |
 如图,六位朋友均匀的围坐在圆桌旁聚会.圆桌的半径为80cm,每人离桌边10cm,有后来两位客人,每人向后挪动了相同距离并左右调整位置,使8个人都坐下,每相邻两人之间的距离与原来相邻两人之间的距离(即在圆周上两人之间的圆弧的长)相等.设每人向后挪动的距离为xcm.则根据题意,可列方程为:
如图,六位朋友均匀的围坐在圆桌旁聚会.圆桌的半径为80cm,每人离桌边10cm,有后来两位客人,每人向后挪动了相同距离并左右调整位置,使8个人都坐下,每相邻两人之间的距离与原来相邻两人之间的距离(即在圆周上两人之间的圆弧的长)相等.设每人向后挪动的距离为xcm.则根据题意,可列方程为: