题目内容
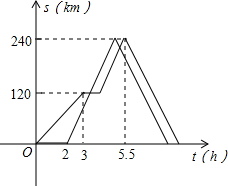 甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,比甲早30分钟到达.到达B地后,乙按原速度返回A地,甲以2a千米/时的速度返回A地.设甲、乙两车与A地相距s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,比甲早30分钟到达.到达B地后,乙按原速度返回A地,甲以2a千米/时的速度返回A地.设甲、乙两车与A地相距s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
(1)求a的值.
(2)求甲车维修所用时间.
(3)求两车在途中第二次相遇时t的值.
(4)当两车相距40千米时,t的取值范围是______.
解:(1)由函数图象,得
a=120÷3=40
(2)由题意,得
5.5-3-120÷(40×2),
=2.5-1.5,
=1.
∴甲车维修的时间为1小时;
(3)∵甲车维修的时间是1小时,
∴B(4,120).
∵乙在甲出发2小时后匀速前往B地,比甲早30分钟到达.
∴E(5,240).
∴乙行驶的速度为:240÷3=80,
∴乙返回的时间为:240÷80=3,
∴F(8,0).
设BC的解析式为y1=k1t+b1,EF的解析式为y2=k2t+b2,由图象,得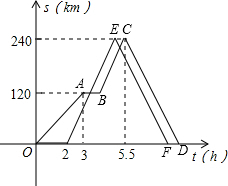
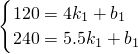 ,
,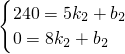 ,
,
解得: ,
,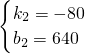 ,
,
∴y1=80t-200,y2=-80t+640,
当y1=y2时,
80t-200=-80t+640,
t=5.25.
∴两车在途中第二次相遇时t的值为5.25小时,
(4)设乙车出发x小时时与甲车相距40km,由题意及函数图象,得
120-40=80x,或80x-120=40
x=1,或x=2,
∴t=3,t=4.
∴由图象得:4<t≤5或5.5≤t≤8时,
综上所述,当t=3,4≤t≤5或5.5≤t≤8时两车相距40千米.
故答案为:t=3,4≤t≤5或5.5≤t≤8
分析:(1)由图象的数量关系,由速度=路程÷时间就可以直接求出结论;
(2)先由图象求出条件求出行驶后面路程的时间久可以求出维修用的时间;
(3)由图象求出BC和EF的解析式,然后由其解析式构成二元一次方程组就可以求出t的值;
(4)设乙车出发x小时时与甲车相距40km,通过函数图象有120-40=80x,或80x-120=40,可以求出t值,根据后面甲、乙速度相等而在维修好后甲乙之间刚好相距40,根据函数图象可以求出t的取值范围.
点评:本题是一道一次函数的综合试题,考查了行程问题的数量关系的运用,追击问题的运用,待定系数法求一次函数的解析式的运用,一次函数与二元一次方程组的运用,解答时第四问时难点,需要用到追击问题的数量关系建立方程求解.
a=120÷3=40
(2)由题意,得
5.5-3-120÷(40×2),
=2.5-1.5,
=1.
∴甲车维修的时间为1小时;
(3)∵甲车维修的时间是1小时,
∴B(4,120).
∵乙在甲出发2小时后匀速前往B地,比甲早30分钟到达.
∴E(5,240).
∴乙行驶的速度为:240÷3=80,
∴乙返回的时间为:240÷80=3,
∴F(8,0).
设BC的解析式为y1=k1t+b1,EF的解析式为y2=k2t+b2,由图象,得

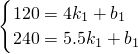 ,
,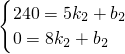 ,
,解得:
 ,
,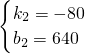 ,
,∴y1=80t-200,y2=-80t+640,
当y1=y2时,
80t-200=-80t+640,
t=5.25.
∴两车在途中第二次相遇时t的值为5.25小时,
(4)设乙车出发x小时时与甲车相距40km,由题意及函数图象,得
120-40=80x,或80x-120=40
x=1,或x=2,
∴t=3,t=4.
∴由图象得:4<t≤5或5.5≤t≤8时,
综上所述,当t=3,4≤t≤5或5.5≤t≤8时两车相距40千米.
故答案为:t=3,4≤t≤5或5.5≤t≤8
分析:(1)由图象的数量关系,由速度=路程÷时间就可以直接求出结论;
(2)先由图象求出条件求出行驶后面路程的时间久可以求出维修用的时间;
(3)由图象求出BC和EF的解析式,然后由其解析式构成二元一次方程组就可以求出t的值;
(4)设乙车出发x小时时与甲车相距40km,通过函数图象有120-40=80x,或80x-120=40,可以求出t值,根据后面甲、乙速度相等而在维修好后甲乙之间刚好相距40,根据函数图象可以求出t的取值范围.
点评:本题是一道一次函数的综合试题,考查了行程问题的数量关系的运用,追击问题的运用,待定系数法求一次函数的解析式的运用,一次函数与二元一次方程组的运用,解答时第四问时难点,需要用到追击问题的数量关系建立方程求解.

练习册系列答案
相关题目
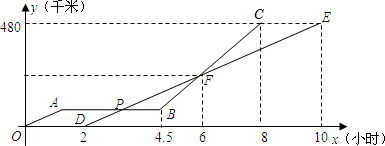
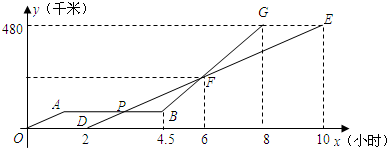
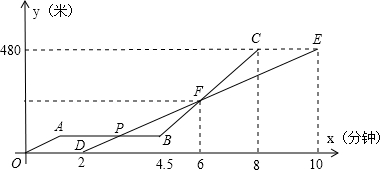
 、线段
、线段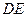 分别表示甲、乙两车所行路程
分别表示甲、乙两车所行路程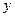 (千米)与时间
(千米)与时间 (小时)之间的函数关系对应的图象(线段
(小时)之间的函数关系对应的图象(线段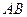 表示甲出发不足2小时因故停车检修).请根据图象所提供的信息,解决如下问题:
表示甲出发不足2小时因故停车检修).请根据图象所提供的信息,解决如下问题: