Question

【题目】如图，已知抛物线y=x2﹣2x﹣3与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，该抛物线顶点为D，对称轴交x轴于点H．

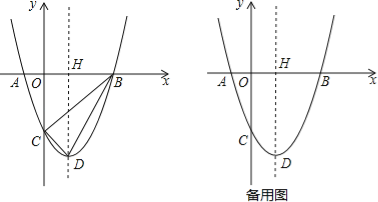
（1）求A，B两点的坐标；

（2）设点P在x轴下方的抛物线上，当∠ABP=∠CDB时，求出点P的坐标；

（3）以OB为边最第四象限内作等边△OBM．设点E为x轴的正半轴上一动点（OE＞OH），连接ME，把线段ME绕点M顺时针旋转60°得MF，求线段DF的长的最小值．

Answer 1

【答案】（1）A（﹣1，0），B（3，0）；（2）P（2，﹣3）；（3）线段DF的长的最小值存在，最小值是2+．

【解析】试题分析：（1）令y=0，求得关于x的方程x2﹣2x﹣3=0的解即为点A、B的横坐标；

（2）设P（x，x2﹣2x﹣3），根据抛物线解析式求得点D的坐标为D（1，﹣4）；结合坐标与图形的性质求得线段CD=，CB=3，BD=2；所以根据勾股定理的逆定理推知∠BCD=90°，则易推知相似三角形△BCD∽△PNB，由该相似三角形的对应边成比例来求x的值，易得点P的坐标；

（3）正确做出等边△OBM和线段ME所对应的旋转线段MF，如图2．过点B，F作直线交对称轴于点G．构建全等三角形：△EOM≌△FBM，由该全等三角形的性质和图形中相关角间的和差关系得到：

∠OBF=120°为定值，即BF所在直线为定直线．过D点作DK⊥BF，K为垂足线段DF的长的最小值即为DK的长度．

解：（1）令y=0，得x2﹣2x﹣3=0，

解得x1=﹣1，x2=3，

∴A（﹣1，0），B（3，0）

（2）设P（x，x2﹣2x﹣3），

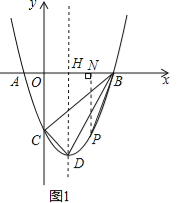
如图1，过点P作PN⊥x轴，垂足为N．

连接BP，设∠NBP=∠CDB．

令x=0，得y=x2﹣2x﹣3=﹣3，

∴C（0，﹣3）

∵y=x2﹣2x﹣3=（x﹣1）2﹣4，

∴D（1，﹣4）．

由勾股定理，得CD=，CB=3，BD=2．

∴BD2=BC2+CD2，

∴∠BCD=90°．

∵∠BCD=∠PNB=90°，∠NBP=∠CDB．

∴△BCD∽△PNB．

∴=，

=，即x2﹣5x+6=0，

解得x1=2，x2=3（不合题意，舍去）．

∴当x=2时，y=﹣3

∴P（2，﹣3）；

（3）正确做出等边△OBM和线段ME所对应的旋转线段MF，如图2．

过点B，F作直线交对称轴于点G．

由题意可得：

，

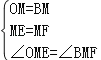∴△EOM≌△FBM，

∴∠MBF=∠MOB=60°．

∵∠OBF=∠OBM+∠MBF=60°+60°=120°为定值，

∴BF所在直线为定直线．

过D点作DK⊥BF，K为垂足．

在Rt△BGH中，∠HBG=180°﹣120°=60°，

∴∠HGB=30°．

∵HB=3，

∴BG=4，HG=2．

∵D（1，﹣4），

∴DH=4，

∴DG=2+4．

在Rt△DGK中，∠DGK=30°．

∴DK=DG=2+．

∵当点E与点H重合时，这时BF=OH=1，

则GF=4+1=5．

而GK=DK=3+2＞5，即点K在点F运动的路径上，

所以线段DF的长的最小值存在，最小值是2+．