题目内容
我们已学会了用“两边夹”的方法，根据不同的精确度要求，估算
的取值范围，我们还可以用“逼近”的方法，求出它的近似值．
2-1.9881=0.0119，2.0164-2=0.0164，0.0119＜0.0164
可见1.9881比2.0164更逼近2，当精确度为0.01时，
的近似值为1.41．
下面，我们用同样的方法估计方程x2+2x=6其中一个解的近似值．
根据上表，方程x2+2x=6的一个解约是
| 2 |
| x | 1.40 | 1.41 | 1.42 | 1.43 | … |
| x2 | 1.96 | 1.9881 | 2.0164 | 2.0449 | … |
可见1.9881比2.0164更逼近2，当精确度为0.01时，
| 2 |
下面，我们用同样的方法估计方程x2+2x=6其中一个解的近似值．
| x | 1.63 | 1.64 | 1.65 | 1.66 | … |
| x2+2x | 5.9169 | 5.9696 | 6.0225 | 6.0756 | … |
1.65
1.65
．（精确到0.01）分析：先根据表中所给的数，再与6相减，然后所得的值进行比较，差值越小的越接近方程的解．
解答：解：根据题意得：
6-5.9696=0.0304，
6.0225-6=0.0225，
0.0304＞0.0225，
可见6.0225比5.9696更逼近6，
当精确度为0.01时，方程x2+2x=6的一个解约是1.65；
故答案为：1.65．
6-5.9696=0.0304，
6.0225-6=0.0225，
0.0304＞0.0225，
可见6.0225比5.9696更逼近6，
当精确度为0.01时，方程x2+2x=6的一个解约是1.65；
故答案为：1.65．
点评：此题考查了估算一元二次方程的近似解，解题的关键是找出表中与6最接近的数，算出差额，再比较，相差越小的数越比较接近．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
我们已学会了用“两边夹”的方法，根据不同的精确度要求，估算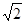
的取值范围，我们还可以用“逼近”的方法，求出它的近似值．
|
x |
1.40 |
1.41 |
1.42 |
1.43 |
… |
|
x2 |
1.96 |
1.9881 |
2.0164 |
2.0449 |
… |
2－1.9881=0.0119，2.0164－2=0.0164，0.0119<0.0164
可见1.9881比2.0164更逼近2，当精确度为0.01时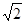，的近似值为1.41．
下面，我们用同样的方法估计方程x2+2x=6其中一个解的近似值．
|
x |
1.63 |
1.64 |
1.65 |
1.66 |
… |
|
x2+2x |
5.9169 |
5.9696 |
6.0225 |
6.0756 |
… |
根据上表，方程x2+2x=6的一个解约是______________．（精确到0.01）
我们已学会了用“两边夹”的方法，根据不同的精确度要求，
估算
的取值范围，我们还可以用“逼近”的方法，求出它的近似值．
| x | 1.40 | 1.41 | 1.42 | 1.43 | … |
| x2 | 1.96 | 1.9881 | 2.0164 | 2.0449 | … |
2－1.9881=0.0119，2.0164－2=0.0164，0.0119<0.0164
可见1.9881比2.0164更逼近2，当精确度为0.01时，的近似值为1.41．
下面，我们用同样的方法估计方程x2+2x=6其中一个解的近似值．
| x | 1.63 | 1.64 | 1.65 | 1.66 | … |
| x2+2x | 5.9169 | 5.9696 | 6.0225 | 6.0756 | … |
根据上表，方程x2+2x=6的一个解约是______________．（精确到0.01）
我们已学会了用“两边夹”的方法，根据不同的精确度要求，估算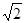
的取值范围，我们还可以用“逼近”的方法，求出它的近似值．
| x | 1.40 | 1.41 | 1.42 | 1.43 | … |
| x2 | 1.96 | 1.9881 | 2.0164 | 2.0449 | … |
可见1.9881比2.0164更逼近2，当精确度为0.01时，
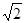的近似值为1.41．下面，我们用同样的方法估计方程x2+2x=6其中一个解的近似值．
| x | 1.63 | 1.64 | 1.65 | 1.66 | … |
| x2+2x | 5.9169 | 5.9696 | 6.0225 | 6.0756 | … |