��Ŀ����
����Ŀ���������Գ��н�����������ģ���ͼ����֪б��AB��90![]() �ף��½ǣ�����BAC��Ϊ45����BC��AC���ּƻ���б���е�D����ȥ����б�£���һ��ƽ����ˮƽ��CA������ƽ̨DE��һ���µ�б��BE��������С�������������ţ���
�ף��½ǣ�����BAC��Ϊ45����BC��AC���ּƻ���б���е�D����ȥ����б�£���һ��ƽ����ˮƽ��CA������ƽ̨DE��һ���µ�б��BE��������С�������������ţ���
��1��������б��BE���±�Ϊ![]() ��1��������ƽ̨DE�ij��Ƕ����ף�
��1��������ƽ̨DE�ij��Ƕ����ף�
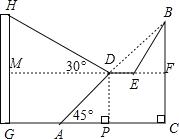
��2��һ��������GH����A��33��Զ����AG=33�ף���С����D���ý����ﶥ��H�����ǣ�����HDM��Ϊ30������B��C��A��G��H��ͬһ��ƽ���ڣ���C��A��G��ͬһ��ֱ���ϣ���HG��CG���ʽ�����GH��Ϊ�����ף�
���𰸡���1����45��15![]() ����2����45+26
����2����45+26![]()
��������
�����������1��������FM��CG�õ���BDF=��BAC=45��������AB�ij��Ⱥ͵�DΪ�е�õ�BD�ij��ȣ�Ȼ�����DF��BF�ij��ȣ�����б��BE���±ȵó�EF�ij��ȣ�Ȼ�����DE=DF��EF�������2������CH=x����MH=x��45��DM=78������Rt��DMH��tan30����ֵ�ó�x��ֵ.
�����������1������FM��CG��
���BDF=��BAC=45����
��б��AB��90![]() �ף�D��AB���е㣬
�ף�D��AB���е㣬
��BD=45![]() �ף�
�ף�
��DF=BDcos��BDF=45![]() ��
��![]() =45���ף���BF=DF=45�ף�
=45���ף���BF=DF=45�ף�
��б��BE���±�Ϊ![]() ��1��
��1��
��EF=15![]() ���ף�
���ף�
��DE=DF��EF=45��15![]() ���ף���
���ף���
������ƽ̨DE�ij��ǣ�45��15![]() ���ף�
���ף�
��2������GH=x�ף���MH=GH��GM=x��45���ף���DM=AG+AP=33+45=78���ף���
��Rt��DMH��tan30��=![]() ��
��
��![]() ��
��
��ã�x=45+26![]() ��
��
�𣺽�����GH�ĸ�Ϊ��45+26![]() ���ף�
���ף�

����Ŀ�������¼��һ����Ա�ڷ������Ϸ����Ľ����
Ͷ������n | 100 | 150 | 300 | 500 | 800 | 1000 |
Ͷ�д���m | 58 | 96 | 174 | 302 | 484 | 601 |
Ͷ��Ƶ�� | 0.580 | 0.640 | 0.580 | 0.604 | 0.605 | 0.601 |
������ԱͶ��һ�Σ�Ͷ�еĸ���Լ��________��