题目内容
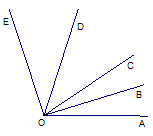
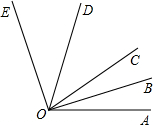 如图已知∠AOE=110°,射线OD、OB分别是∠EOC、∠COA的角平分线.则∠BOD的度数是
如图已知∠AOE=110°,射线OD、OB分别是∠EOC、∠COA的角平分线.则∠BOD的度数是55°
55°
;若以OB为钟表上的时针,OD为分针,且OB在2小时~3小时之间,请写出此刻的时间2时
分.
| 10 |
| 11 |
2时
分.
.| 10 |
| 11 |
分析:(1)根据已知条件即可推出∠BOD=
∠AOE,通过计算即可推出的结果;
(2)若以OB为钟表上的时针,OD为分针,则∠DOB为时针与分针的夹角为55°,设2时转成55°的时间为x分,则12x+60-6x=55,解方程求出x即可推出结果.
| 1 |
| 2 |
(2)若以OB为钟表上的时针,OD为分针,则∠DOB为时针与分针的夹角为55°,设2时转成55°的时间为x分,则12x+60-6x=55,解方程求出x即可推出结果.
解答:解:(1)∵射线OD、OB是∠EOC、∠COA的角平分线,
∴∠DOB=
∠EOC+
∠AOC=
(∠EOC+∠AOC)=
∠AOE=55°;
(2)若以OB为钟表上的时针,OD为分针,则∠DOB为时针与分针的夹角为55°,
设2时转成55°的时间为x分,
∴
x+60-6x=55
∴5.5x=5
∴x=
,
即时间为2时
分.
故答案为55°,2时
分.
∴∠DOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)若以OB为钟表上的时针,OD为分针,则∠DOB为时针与分针的夹角为55°,
设2时转成55°的时间为x分,
∴
| 1 |
| 2 |
∴5.5x=5
∴x=
| 10 |
| 11 |
即时间为2时
| 10 |
| 11 |
故答案为55°,2时
| 10 |
| 11 |
点评:本题考查了角平分线的定义以及钟面角问题,时钟问题的关键是将时针、分针、秒针转动的速度用角表示出来,时针转动的速度为0.5°/分,分针为6°/分,秒针为360°/分,难度适中.

练习册系列答案
相关题目
 如图已知FB∥ED,AB∥DC,∠B=50°,求∠D的度数.
如图已知FB∥ED,AB∥DC,∠B=50°,求∠D的度数.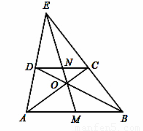
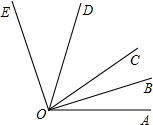 如图已知∠AOE=110°,射线OD、OB分别是∠EOC、∠COA的角平分线.则∠BOD的度数是________;若以OB为钟表上的时针,OD为分针,且OB在2小时~3小时之间,请写出此刻的时间________.
如图已知∠AOE=110°,射线OD、OB分别是∠EOC、∠COA的角平分线.则∠BOD的度数是________;若以OB为钟表上的时针,OD为分针,且OB在2小时~3小时之间,请写出此刻的时间________.