题目内容
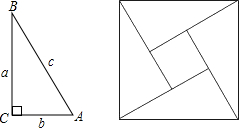 如图为2002年国际数学家大会的会标,它可以看成由四个形状、大小完全相同的直角三角形拼成(其中较大的直角边长为a,较小的直角边长为b,斜边长为c),根据此图,回答下列问题:
如图为2002年国际数学家大会的会标,它可以看成由四个形状、大小完全相同的直角三角形拼成(其中较大的直角边长为a,较小的直角边长为b,斜边长为c),根据此图,回答下列问题:
(1)请你通过不同方法计算中间小正方形的面积,并得出一个等式.
(2)你能用一句话概括这个结论吗?
(3)利用刚才的结论解决下面的问题:已知一个直角三角形的两直角边为5和12,试问斜边上的高为多少?
解:(1)设中间小正方形的面积为S,
根据题意得:S=c2-4× ab=c2-2ab;S=(a-b)2=a2-2ab+b2,
ab=c2-2ab;S=(a-b)2=a2-2ab+b2,
∴c2-2ab=a2-2ab+b2,即c2=a2+b2;
(2)直角三角形两直角边的平方和等于斜边的平方;
(3)∵直角三角形两直角边分别为5和12,
∴斜边为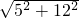 =13,
=13,
∵三角形的面积S= ×5×12=
×5×12= ×13h,
×13h,
则斜边上的高h=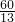 .
.
分析:(1)中间小正方形的面积有两种求法,一种是直接求,由直角三角形长直角边减去短直角边,得到小正方形的边长,利用正方形的面积公式表示出S;一种是间接求,用大正方形的面积减去四个直角三角形的面积,两种求法求出的面积相等,列出等式;
(2)直角三角形两直角边的平方和等于斜边的平方;
(3)利用此结论求出斜边的长,利用面积法即可求出斜边上的高.
点评:此题考查了整式混合运算的应用,属于探究型试题,弄清题意是解本题的关键.
根据题意得:S=c2-4×
 ab=c2-2ab;S=(a-b)2=a2-2ab+b2,
ab=c2-2ab;S=(a-b)2=a2-2ab+b2,∴c2-2ab=a2-2ab+b2,即c2=a2+b2;
(2)直角三角形两直角边的平方和等于斜边的平方;
(3)∵直角三角形两直角边分别为5和12,
∴斜边为
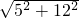 =13,
=13,∵三角形的面积S=
 ×5×12=
×5×12= ×13h,
×13h,则斜边上的高h=
 .
.分析:(1)中间小正方形的面积有两种求法,一种是直接求,由直角三角形长直角边减去短直角边,得到小正方形的边长,利用正方形的面积公式表示出S;一种是间接求,用大正方形的面积减去四个直角三角形的面积,两种求法求出的面积相等,列出等式;
(2)直角三角形两直角边的平方和等于斜边的平方;
(3)利用此结论求出斜边的长,利用面积法即可求出斜边上的高.
点评:此题考查了整式混合运算的应用,属于探究型试题,弄清题意是解本题的关键.

练习册系列答案
相关题目
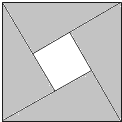 如图是2002年8月在北京召开的第24届国际数学家大会会标的图形,它由四个相同的直角三角形拼合而成.若大正方形的面积为13,每个直角三角形直角边的和是5,则中间小正方形的面积为
如图是2002年8月在北京召开的第24届国际数学家大会会标的图形,它由四个相同的直角三角形拼合而成.若大正方形的面积为13,每个直角三角形直角边的和是5,则中间小正方形的面积为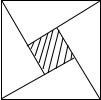 如图是2002年8月在北京召开的第24届国际数学家大会的会标,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积为13,小正方形的面积是1,直角三角形较长的直角边为a,较短的直角边为b,则a4+b3的值等于
如图是2002年8月在北京召开的第24届国际数学家大会的会标,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积为13,小正方形的面积是1,直角三角形较长的直角边为a,较短的直角边为b,则a4+b3的值等于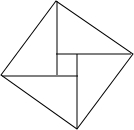 如图是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,若图中大小正方形的面积分别为52和4,则直角三角形的两直角边分别为
如图是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,若图中大小正方形的面积分别为52和4,则直角三角形的两直角边分别为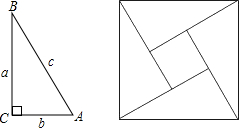 如图为2002年国际数学家大会的会标,它可以看成由四个形状、大小完全相同的直角三角形拼成(其中较大的直角边长为a,较小的直角边长为b,斜边长为c),根据此图,回答下列问题:
如图为2002年国际数学家大会的会标,它可以看成由四个形状、大小完全相同的直角三角形拼成(其中较大的直角边长为a,较小的直角边长为b,斜边长为c),根据此图,回答下列问题: