Question

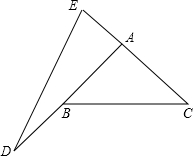
如图，在等腰三角形ABC中，延长AB到点D，延长CA到点E，且AE=BD，连接DE．如果AD=BC=CE=DE，求∠BAC的度数．

Answer 1

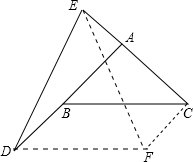
过D作DF∥BC，且使DF=BC，连CF、EF，则四边形BDFC是平行四边形，
∴BD=CF，DA∥FC，
∴∠EAD=∠ECF，
∵AD=CE，AE=BD=CF，
∴△ADE≌△CEF（SAS）
∴ED=EF，
∵ED=BC，BC=DF，
∴ED=EF=DF
∴△DEF为等边三角形
设∠BAC=x°，则∠ADF=∠ABC=

180°-x°

2

，
∴∠DAE=180°-x°，
∴∠ADE=180°-2∠DAE=180°-2（180°-x°）=2x°-180°，
∵∠ADF+∠ADE=∠EDF=60°
∴

180°-x°

2

+（2x°-180°）=60°
∴x=100．
∴∠BAC=100°．