题目内容
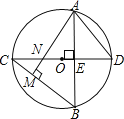
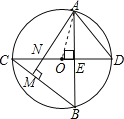
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.
(1)求证:AD=AN;
(2)若AB=![]() ,ON=1,求⊙O的半径.
,ON=1,求⊙O的半径.
(3)若![]() 且AE=4,求CM
且AE=4,求CM
【答案】(1)、证明过程见解析;(2)、3;(3)、CM=2.
【解析】
试题分析:(1)、根据同弧所对的圆周角相等得出∠B=∠D,根据双垂直得出∠B=∠ANE,从而得出∠D=∠ANE,从而得到答案;(2)、设NE=x,则OE=x-1,ED=x,r=2x-1,根据Rt△AOE的勾股定理得出x的值,从而求出半径;(3)、根据△ANE的面积等于△ADE的面积以及S△CMN:S△AND=1:8,从而得出S△CMN:S△ANE=1:4,求出答案.
试题解析:(1)、根据图示可得:∠B=∠D ∵AM⊥BC,AB⊥CD ∴∠B=∠ANE
∴∠ANE=∠D ∴AD=AN
(2)、∵AB=![]() ,AE⊥CD,∴AE=
,AE⊥CD,∴AE=![]() ,又∵ON=1,∴设NE=x,则OE=x-1,NE=ED=x,
,又∵ON=1,∴设NE=x,则OE=x-1,NE=ED=x,
r=OD=OE+ED=2x-1 连结AO,则AO=OD=2x-1,
∵△AOE是直角三角形,AE=![]() ,OE=x-1,AO=2x-1, ∴
,OE=x-1,AO=2x-1, ∴![]()
解得x=2,∴r=2x-1=3.
(3)、∵AD=AN,AB⊥CD,∴AE平分ND,∴S△ANE=S△ADE ∵S△CMN:S△AND=1:8,∴S△CMN:S△ANE=1:4,
又∵△CMN∽△AEN,∴![]() ∵AE=4,∴CM=2
∵AE=4,∴CM=2

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目