题目内容
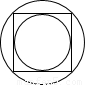
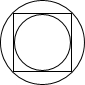 如图,一正方形同时外切和内接于两个同心圆,当小圆的半径为r时,大圆的半径为
如图,一正方形同时外切和内接于两个同心圆,当小圆的半径为r时,大圆的半径为
- A.
 r
r - B.1.5r
- C.
 r
r - D.2r
A
分析:首先连接OD、OE、OF,构造正方形OEDF,证出四边形OEDF是正方形,根据勾股定理求出斜边即可.
解答: 解:如图,连接OD、OE、OF,
解:如图,连接OD、OE、OF,
则:OE=OF=r,
∵正方形ABCD切小圆于E、F,
∴∠OED=∠OFD=∠D=90°,
∴四边形OEDF是正方形,
∴OE=DE=r,
在△OED中由勾股定理得:OD=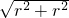 =
= r,
r,
即大圆的半径是 r.
r.
故选A.
点评:本题主要考查了正多边形和圆,正方形的判定和性质,勾股定理,切线的性质等知识点,解此题的关键是确定大圆的半径、小圆的半径、边长之间的关系.
分析:首先连接OD、OE、OF,构造正方形OEDF,证出四边形OEDF是正方形,根据勾股定理求出斜边即可.
解答:
 解:如图,连接OD、OE、OF,
解:如图,连接OD、OE、OF,则:OE=OF=r,
∵正方形ABCD切小圆于E、F,
∴∠OED=∠OFD=∠D=90°,
∴四边形OEDF是正方形,
∴OE=DE=r,
在△OED中由勾股定理得:OD=
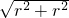 =
= r,
r,即大圆的半径是
 r.
r.故选A.
点评:本题主要考查了正多边形和圆,正方形的判定和性质,勾股定理,切线的性质等知识点,解此题的关键是确定大圆的半径、小圆的半径、边长之间的关系.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
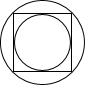 如图,一正方形同时外切和内接于两个同心圆,当小圆的半径为r时,大圆的半径为( )
如图,一正方形同时外切和内接于两个同心圆,当小圆的半径为r时,大圆的半径为( )A、
| ||
| B、1.5r | ||
C、
| ||
| D、2r |

 r
r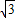 r
r