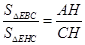题目内容
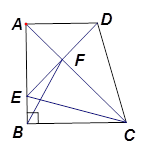
在直角梯形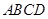 中,
中,![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() ,且
,且![]() .连接
.连接![]() 交对角线
交对角线![]() 于
于![]() ,连接
,连接![]() .下列结论:
.下列结论:
①![]() ;②
;②![]() 为等边三角形;
为等边三角形;
③![]() ; ④
; ④![]() . 其中结论正确的是
. 其中结论正确的是
A.只有①② B.只有①②④
C.只有③④ D.①②③④
B
解析:由题意可知△ACD和△ACE全等,故①正确;
又因为∠BCE=15°,所以∠ACE=45°﹣15°=30°,所以∠ECD=60°,所以△CDE是等边三角形,故②正确;
∵AE=AE,△ACD≌△ACE,△CDE是等边三角形,
∴∠EAH=∠AHD=45°,AD=AE,
∴AH=EH=DH,AH⊥DE,
假设AH=EH=DH=x,
∴AE=![]() x,CE=2x,
x,CE=2x,
∴CH=![]() x,
x,
∴AC=(1+![]() )x,
)x,
∵AB=BC,
∴AB2+BC2=[(1+![]() )x]2,
)x]2,
解得:AB=![]() x,
x,
BE=![]() x,
x,
∴![]() =
=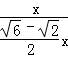 =
=![]() ,
,
故③错误;
④∵Rt△EBC与Rt△EHC共斜边EC,
∴S△EBC:S△EHC=(BE×BC):(HE×HC)
=(EC×sin15°×EC×cos15°):(EC×sin30°×EC×cos30°)
=(EC×sin30°):(EC×sin60°)
=EH:CH
=AH:CH,故此选项正确.
故其中结论正确的是①②④.
故选B.

练习册系列答案
相关题目
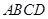 中,
中,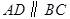 ,
,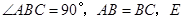 为
为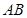 边上一点,
边上一点,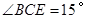 ,且
,且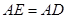 .连接
.连接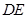 交对角线
交对角线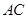 于
于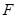 ,连接
,连接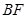 .下列结论:
.下列结论: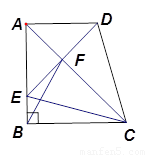
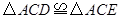 ;②
;②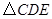 为等边三角形;
为等边三角形;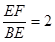 ; ④
; ④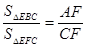 . 其中结论正确的是
. 其中结论正确的是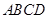 中,
中,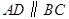 ,
,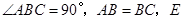 为
为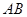 边上一点,
边上一点,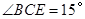 ,且
,且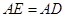 .连接
.连接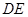 交对角线
交对角线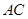 于
于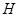 ,连接
,连接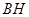 .下列结论:
.下列结论: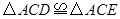 ;②
;②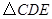 为等边三角形;③
为等边三角形;③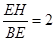 ;
④.
;
④.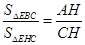

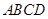 中,
中,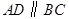 ,
,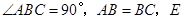 为
为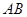 边上一点,
边上一点,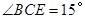 ,且
,且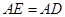 .连接
.连接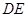 交对角线
交对角线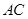 于
于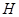 ,连接
,连接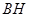 .下列结论:
.下列结论:
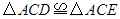 ;②
;②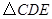 为等边三角形;
为等边三角形;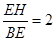 ;
④
;
④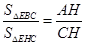 .其中结论正确的是
.其中结论正确的是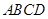 中,
中,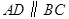 ,
,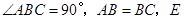 为
为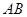 边上一点,
边上一点,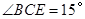 ,且
,且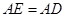 .连接
.连接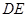 交对角线
交对角线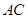 于
于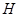 ,连接
,连接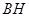 .下列结论:
.下列结论: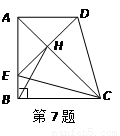 ①
①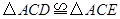 ;②
;②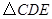 为等边三角形;
为等边三角形;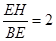 ; ④
; ④