题目内容
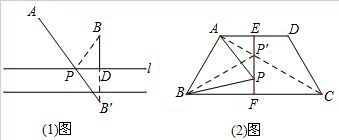
唐朝诗人李欣的诗《古从军行》开头两句说:“白日登山望峰火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题--将军饮马问题:如图1所示,诗中将军在观望烽火之后从山脚下的A点出发,走到河旁边的P点饮马后再到B点宿营.请问怎样走才能使总的路程最短?
做法如下:如图1,从B出发向河岸引垂线,垂足为D,在AD的延长线上,取B关于河岸的对称点B′,连接AB′,与河岸线相交于P,则P点就是饮马的地方,将军只要从A出发,沿直线走到P,饮马之后,再由P沿直线走到B,所走的路程就是最短的.
(1)观察发现
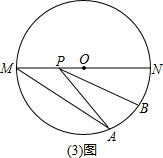
再如图2,在等腰梯形ABCD中,AB=CD=AD=2,∠D=120°,点E、F是底边AD与BC的中点,连接EF,在线段EF上找一点P,使BP+AP最短.
作点B关于EF的对称点,恰好与点C重合,连接AC交EF于一点,则这点就是所求的点P,故BP+AP的最小值为______
【答案】分析:(1)联系题干给出的信息提示,在等腰梯形ABCD中,B、C关于直线EF对称,所以BP+AP的最小值应为线段AC的长,所以只需求出AC长即可;梯形ABCD中,AD∥BC,所以同旁内角∠BAD、∠ABC互补,已知∠BAD=∠D=120°,所以∠ABC=60°,在等腰△ADC中(AD=CD=2),易求得底角∠DAC=30°,此时可以发现△BAC是含30°角的特殊直角三角形,已知AB的长,则线段AC的长可得,由此得解.
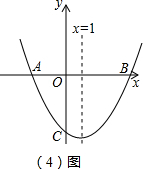
(2)延续上面的思路,先作点A关于直径MN的对称点C,连接BC,那么BC与MN的交点即符合点P的要求,BP+AP的最小值应是弦BC的长;已知点B是劣弧AN的中点,所以圆周角∠AMN= ∠AON=∠BON=30°;点A、C关于直径MN对称,那么
∠AON=∠BON=30°;点A、C关于直径MN对称,那么 =
= ,因此∠CON=∠AON=60°,由此可以看出△BOC是一个等腰直角三角形,已知⊙O的直径可得半径长,则等腰直角三角形的斜边(即BP+AP的最小值BC长)可求.
,因此∠CON=∠AON=60°,由此可以看出△BOC是一个等腰直角三角形,已知⊙O的直径可得半径长,则等腰直角三角形的斜边(即BP+AP的最小值BC长)可求.
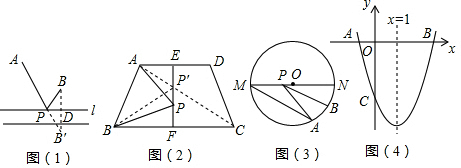
(3)①已知抛物线对称轴x= =1,以及点A、C的坐标,由待定系数法能求出抛物线的解析式;
=1,以及点A、C的坐标,由待定系数法能求出抛物线的解析式;
②△ACM中,点A、C的坐标已确定,所以边AC的长是定值,若△ACM的周长最小,那么AM+CM的值最小,所以此题的思路也可以延续上面两题的思路;过点C作x轴的平行线,交抛物线于另一点D,根据抛物线的对称性点D的坐标易得,首先利用待定系数法求出直线AD的解析式,那么直线AD与抛物线对称轴的交点就是符合条件的点M;在求出点A、C、D三点的坐标后,线段AC、AD的长可得,所以△ACM的周长最小值=AC+AD(其中AD为AM+CM的最小值).
解答:解:(1)在等腰梯形ABCD中,∵AD∥BC,且∠BAD=∠D=120°,
∴∠ABC=60°;
在△ADC中,AD=CD=2,∠D=120°,所以∠DAC=∠DCA=30°;
∴∠BAC=∠BAD-∠DAC=120°-30°=90°,即△BAC为直角三角形;
在Rt△BAC中,∠ABC=60°,∠BCA=90°-60°=30°,AB=2,所以AC=AB•tan60°=2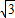 ;
;
由于B、C关于直线EF对称,根据阅读资料可知BP+AP的最小值为线段AC的长,即2 .
.
 (2)如图(2),作点A关于直径MN的对称点C,连接BC,则BC与直径MN的交点为符合条件的点P,BC的长为BP+AP的最小值;
(2)如图(2),作点A关于直径MN的对称点C,连接BC,则BC与直径MN的交点为符合条件的点P,BC的长为BP+AP的最小值;
连接OA,则∠AON=2∠AMN=60°;
∵点B是 的中点,
的中点,
∴∠BON= ∠AON=30°;
∠AON=30°;
∵A、C关于直径MN对称,
∴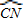 =
= ,则∠CON=∠AON=60°;
,则∠CON=∠AON=60°;
∴∠BOC=∠BON+∠CON=90°,又OC=OB= MN=
MN= ,
,
在等腰Rt△BOC中,BC= OB=
OB= ;
;
即:BP+AP的最小值为 .
.
 (3)①依题意,有:
(3)①依题意,有:
 ,解得
,解得
∴抛物线的解析式:y=x2-2x-3;
②取点C关于抛物线对称轴x=1的对称点D,根据抛物线的对称性,得:D(2,-3);
连接AD,交抛物线的对称轴于点M,如图(3)-②;
设直线AD的解析式为y=kx+b,代入A(-1,0)、D(2,-3),得:
 ,解得
,解得
∴直线AD:y=-x-1,M(1,-2);
∴△ACM的周长最小值:lmin=AC+AD= +3
+3 .
.
点评:此题主要考查了:等腰梯形的性质、圆周角定理、解直角三角形、利用待定系数法确定二次函数解析式等综合知识;题目的三个小题都是题干阅读信息的实际应用,解题的关键是阅读信息中得到的结论,这就要充分理解轴对称图形的性质以及两点间线段最短的具体含义.
(2)延续上面的思路,先作点A关于直径MN的对称点C,连接BC,那么BC与MN的交点即符合点P的要求,BP+AP的最小值应是弦BC的长;已知点B是劣弧AN的中点,所以圆周角∠AMN=
 ∠AON=∠BON=30°;点A、C关于直径MN对称,那么
∠AON=∠BON=30°;点A、C关于直径MN对称,那么 =
= ,因此∠CON=∠AON=60°,由此可以看出△BOC是一个等腰直角三角形,已知⊙O的直径可得半径长,则等腰直角三角形的斜边(即BP+AP的最小值BC长)可求.
,因此∠CON=∠AON=60°,由此可以看出△BOC是一个等腰直角三角形,已知⊙O的直径可得半径长,则等腰直角三角形的斜边(即BP+AP的最小值BC长)可求.(3)①已知抛物线对称轴x=
 =1,以及点A、C的坐标,由待定系数法能求出抛物线的解析式;
=1,以及点A、C的坐标,由待定系数法能求出抛物线的解析式;②△ACM中,点A、C的坐标已确定,所以边AC的长是定值,若△ACM的周长最小,那么AM+CM的值最小,所以此题的思路也可以延续上面两题的思路;过点C作x轴的平行线,交抛物线于另一点D,根据抛物线的对称性点D的坐标易得,首先利用待定系数法求出直线AD的解析式,那么直线AD与抛物线对称轴的交点就是符合条件的点M;在求出点A、C、D三点的坐标后,线段AC、AD的长可得,所以△ACM的周长最小值=AC+AD(其中AD为AM+CM的最小值).
解答:解:(1)在等腰梯形ABCD中,∵AD∥BC,且∠BAD=∠D=120°,
∴∠ABC=60°;
在△ADC中,AD=CD=2,∠D=120°,所以∠DAC=∠DCA=30°;
∴∠BAC=∠BAD-∠DAC=120°-30°=90°,即△BAC为直角三角形;
在Rt△BAC中,∠ABC=60°,∠BCA=90°-60°=30°,AB=2,所以AC=AB•tan60°=2
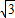 ;
;由于B、C关于直线EF对称,根据阅读资料可知BP+AP的最小值为线段AC的长,即2
 .
. (2)如图(2),作点A关于直径MN的对称点C,连接BC,则BC与直径MN的交点为符合条件的点P,BC的长为BP+AP的最小值;
(2)如图(2),作点A关于直径MN的对称点C,连接BC,则BC与直径MN的交点为符合条件的点P,BC的长为BP+AP的最小值;连接OA,则∠AON=2∠AMN=60°;
∵点B是
 的中点,
的中点,∴∠BON=
 ∠AON=30°;
∠AON=30°;∵A、C关于直径MN对称,
∴
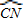 =
= ,则∠CON=∠AON=60°;
,则∠CON=∠AON=60°;∴∠BOC=∠BON+∠CON=90°,又OC=OB=
 MN=
MN= ,
,在等腰Rt△BOC中,BC=
 OB=
OB= ;
;即:BP+AP的最小值为
 .
. (3)①依题意,有:
(3)①依题意,有: ,解得
,解得
∴抛物线的解析式:y=x2-2x-3;
②取点C关于抛物线对称轴x=1的对称点D,根据抛物线的对称性,得:D(2,-3);
连接AD,交抛物线的对称轴于点M,如图(3)-②;
设直线AD的解析式为y=kx+b,代入A(-1,0)、D(2,-3),得:
 ,解得
,解得
∴直线AD:y=-x-1,M(1,-2);
∴△ACM的周长最小值:lmin=AC+AD=
 +3
+3 .
.点评:此题主要考查了:等腰梯形的性质、圆周角定理、解直角三角形、利用待定系数法确定二次函数解析式等综合知识;题目的三个小题都是题干阅读信息的实际应用,解题的关键是阅读信息中得到的结论,这就要充分理解轴对称图形的性质以及两点间线段最短的具体含义.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目