题目内容
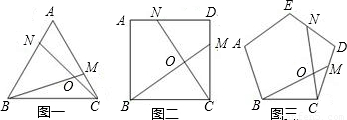
7、如图，在正五边形ABCDE中，对角线AD，AC与EB分别相交于点M，N．下列结论错误的是（ ）分析：首先由正五边形的性质可得AB=BC=CD=DE=AE，BE∥CD，AD∥BC，AC∥DE，AC=AD=BE，根据有一组邻边相等的平行四边形是菱形即可证得A正确，根据等腰梯形的判定方法即可证得B正确，利用SSS即可判定D正确，利用排除法即可求得答案．
解答：解：∵在正五边形ABCDE中，
∴AB=BC=CD=DE=AE，BE∥CD，AD∥BC，AC∥DE，
∴四边形EDCN是平行四边形，
∴?EDCN是菱形；故A正确；
同理：四边形BCDM是菱形，
∴CN=DE，DM=BC，
∴CN=DM，
∴四边形MNCD是等腰梯形，故B正确；
∴EN=ED=DM=AE=CN=BM=CD，
∵AN=AC-CN，EM=BE-BM，
∵BE=AC，
∴△AEN≌△EDM（SSS），故D正确．
故选C．
∴AB=BC=CD=DE=AE，BE∥CD，AD∥BC，AC∥DE，
∴四边形EDCN是平行四边形，
∴?EDCN是菱形；故A正确；
同理：四边形BCDM是菱形，
∴CN=DE，DM=BC，
∴CN=DM，
∴四边形MNCD是等腰梯形，故B正确；
∴EN=ED=DM=AE=CN=BM=CD，
∵AN=AC-CN，EM=BE-BM，
∵BE=AC，
∴△AEN≌△EDM（SSS），故D正确．
故选C．
点评：此题考查了正五边形的性质，菱形的判定与性质，等腰梯形的判定与性质以及全等三角形的判定等知识．此题综合性很强，注意数形结合思想的应用．
练习册系列答案
相关题目
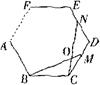
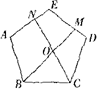
，若∠BON=108°，请问结论BM=CN是否还成立？若成立，请给予证明；若不成立，请说明理由．
