题目内容
23、一列火车自A城驶往B城,沿途有n个车站(包括起点站A和终点站B),该列火车挂有一节邮政车厢,运行时需要在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该站的邮包一个,还要装上该站发往下面行程中每个车站的邮包一个.
例如,当列车停靠在第x个车站时,邮政车厢上需要卸下已经通过的(x-1)个车站发给该站的邮包共(x-1)个,还要装上下面行程中要停靠的(n-x)个车站的邮包共(n-x)个.
(1)根据题意,完成下表:
(2)根据上表,写出列车在第x车站启程时,邮政车厢上共有邮包的个数y(用x、n表示);
(3)当n=18时,列车在第几个车站启程时邮政车厢上邮包的个数最多?
例如,当列车停靠在第x个车站时,邮政车厢上需要卸下已经通过的(x-1)个车站发给该站的邮包共(x-1)个,还要装上下面行程中要停靠的(n-x)个车站的邮包共(n-x)个.
(1)根据题意,完成下表:
| 车站序号 | 在第x个车站起程时邮政车厢邮包总数 |
| 1 | n-1 |
| 2 | (n-1)-1+(n-2)=2(n-2) |
| 3 | 2(n-2)-2+(n-3)=3(n-3) |
| 4 | |
| 5 | |
| … | … |
| n |
(3)当n=18时,列车在第几个车站启程时邮政车厢上邮包的个数最多?
分析:(1)随着序号的增加,所有的项也跟着有规律的变化.注意到最后的包裹数为0.
(2)第x个车站,包裹数为:x(n-x)
(3)根据二次函数的最大值来求即可.
(2)第x个车站,包裹数为:x(n-x)
(3)根据二次函数的最大值来求即可.
解答:解:(1)由题意得:
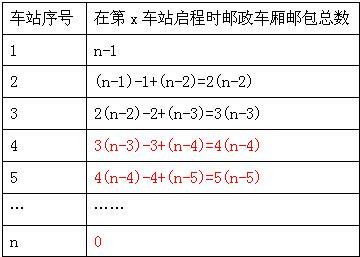
(2)由题意得:y=x(n-x);
(3)当n=18时,y=x(18-x)=-x2+18x=-(x-9)2+81,
当x=9时,y取得最大值.
所以列车在第9个车站启程时,邮政车厢上邮包的个数最多.

(2)由题意得:y=x(n-x);
(3)当n=18时,y=x(18-x)=-x2+18x=-(x-9)2+81,
当x=9时,y取得最大值.
所以列车在第9个车站启程时,邮政车厢上邮包的个数最多.
点评:解决此类探究性问题,关键在观察、分析已知数据,寻找它们之间的相互联系,探寻其规律.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
一列火车自A城驶往B城,沿途有n个车站(包括起点站A和终点站B),该列火车挂有一节邮政车厢,运行时需要在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该站的邮包一个,还要装上该站发往下面行程中每个车站的邮包一个。例如,当列车停靠在第x 个车站时,邮政车厢上需要卸下已经通过的(x-1)个车站发给该站的邮包共(x-1)个,还要装上下面行程中要停靠的(n-x)个车站的邮包共(n-x)个。
(1)根据题意,完成下表:
| 车站序号 | 在第x车站启程时邮政车厢邮包总数 |
| 1 | n-1 |
| 2 | (n-1)-1+(n-2)=2(n-2) |
| 3 | 2(n-2)-2+(n-3)=3(n-3) |
| 4 | |
| 5 | |
| … | …… |
| n | |
n表示)。
(3)当n=18时,列车在第几个车站启程时邮政车厢上邮包的个数最多?