题目内容
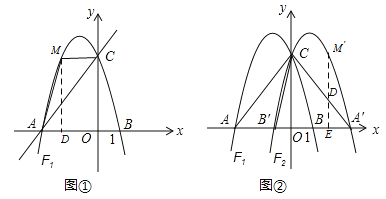
【题目】如图①，直线
交于x轴于点A，交y轴于点C，过A、C两点的抛物线F1交x轴于另一点B（1，0）．
（1）求抛物线F1所表示的二次函数的表达式；
（2）若点M是抛物线F1位于第二象限图象上的一点，设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC，记S=S四边形MAOC﹣S△BOC，求S最大时点M的坐标及S的最大值；
（3）如图②，将抛物线F1沿y轴翻折并“复制”得到抛物线F2，点A、B与（2）中所求的点M的对应点分别为A′、B′、M′，过点M′作M′E⊥x轴于点E，交直线A′C于点D，在x轴上是否存在点P，使得以A′、D、P为顶点的三角形与△AB′C相似？若存在，请求出点P的坐标；若不存在，请说明理由．
【答案】（1）
；（2）当a=
时，S有最大值，最大值为
，此时，M（，5）；（3）P（2，0）或（
，0）．
【解析】
试题分析：（1）利用一次函数的解析式求出点A、C的坐标，然后再利用B点坐标即可求出二次函数的解析式；
（2）由于M在抛物线F1上，所以可设M（a，
），然后分别计算S四边形MAOC和S△BOC，过点M作MD⊥x轴于点D，则S四边形MAOC的值等于△ADM的面积与梯形DOCM的面积之和．
（3）由于没有说明点P的具体位置，所以需要将点P的位置进行分类讨论，当点P在A′的右边时，此情况是不存在；当点P在A′的左边时，此时∠DA′P=∠CAB′，若以A′、D、P为顶点的三角形与△AB′C相似，则分为以下两种情况进行讨论：①
；②
．
试题解析：（1）令y=0代入
，∴x=﹣3，A（﹣3，0），令x=0，代入，∴y=4，∴C（0，4），设抛物线F1的解析式为：y=a（x+3）（x﹣1），把C（0，4）代入上式得，a=
，∴；
（2）如图①，设点M（a，），其中﹣3＜a＜0．
∵B（1，0），C（0，4），∴OB=1，OC=4，∴S△BOC=
OBOC=2，过点M作MD⊥x轴于点D，∴MD=，AD=a+3，OD=﹣a，∴S四边形MAOC=ADMD+（MD+OC）OD=ADMD+ODMD+ODOC=MD（AD+OD）+ ODOC=MDOA+ODOC
=
=
∴S=S四边形MAOC﹣S△BOC=
=
=
∴当a=时，S有最大值，最大值为，此时，M（，5）；
（3）如图②，由题意知：M′（
，5），B′（﹣1，0），A′（3，0），∴AB′=2．
设直线A′C的解析式为：y=kx+b，把A′（3，0）和C（0，4）代入y=kx+b，得：
，∴
，∴
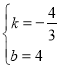，令x=代入，∴y=2，∴D（，2）．由勾股定理分别可求得：AC=5，DA′=
．设P（m，0），①当m＜3时，此时点P在A′的左边，∴∠DA′P=∠CAB′，当时，△DA′P∽△CAB′，此时，
=（3﹣m），解得：m=2，∴P（2，0）；
当时，△DA′P∽△B′AC，此时，=
（3﹣m），解得m=，∴P（，0）
②当m＞3时，此时，点P在A′右边，由于∠CB′O≠∠DA′E，∴∠AB′C≠∠DA′P，∴此情况，△DA′P与△B′AC不能相似．
综上所述，当以A′、D、P为顶点的三角形与△AB′C相似时，点P的坐标为（2，0）或（
，0）．
