题目内容
(2010•高要市二模)已知,如图,等边三角形ABC边长为2,以BC为对称轴将△ABC翻折,得到四边形ABDC,将此四边形放在直角坐标系xOy中,使AB在x轴上,点D在直线 上.
上.(1)根据上述条件画出图形,并求出A、B、D、C的坐标;
(2)若直线
 与y轴交于点P,抛物线y=ax2+bx+c,过A、B、P三点,求这条抛物线的函数关系式;
与y轴交于点P,抛物线y=ax2+bx+c,过A、B、P三点,求这条抛物线的函数关系式;(3)求出抛物线的顶点坐标,并指出这个点在△ABC的什么特殊位置.

【答案】分析:(1)已知了正三角形的边长为2,即可求得D、C的纵坐标为 ,将其代入直线
,将其代入直线 中,即可求得点D的坐标,易知四边形ABDC是菱形,根据菱形的边长为2,以及点D的坐标,即可确定出其他三点的坐标.
中,即可求得点D的坐标,易知四边形ABDC是菱形,根据菱形的边长为2,以及点D的坐标,即可确定出其他三点的坐标.
(2)根据直线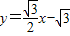 的解析式,易求得点P的坐标,而A、B的坐标在(1)题已经求得,即可利用待定系数法求出该抛物线的解析式.
的解析式,易求得点P的坐标,而A、B的坐标在(1)题已经求得,即可利用待定系数法求出该抛物线的解析式.
(3)可用配方法将(2)题所得函数解析式化为顶点坐标式,进而可求出其顶点坐标,再根据坐标来判断它在△ABC中的特殊位置.
解答: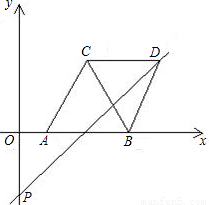 解:(1)依题意,四边形ABDC为菱形,
解:(1)依题意,四边形ABDC为菱形,
∵AB=2,∠CAB=60°,
∴C、D两点纵坐标均为 ;
;
设 ,
,
∵点D在直线 上,
上,
∴ ,
,
∴ ;
;
如图,(4分)
(2) ,抛物线过A、B、P三点,
,抛物线过A、B、P三点,
∴
解得 ;
;
∴ .(6分)
.(6分)
(3) =
= ,
,
∴顶点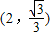 ;(7分)
;(7分)
这个点在△ABC的内心位置.(8分)
(答外心、重心、垂心均可)
点评:此题主要考查了图形的旋转变换、等边三角形的性质、二次函数界限的确定等知识.正确的求出点D的坐标是解决此题的关键,难度适中.
 ,将其代入直线
,将其代入直线 中,即可求得点D的坐标,易知四边形ABDC是菱形,根据菱形的边长为2,以及点D的坐标,即可确定出其他三点的坐标.
中,即可求得点D的坐标,易知四边形ABDC是菱形,根据菱形的边长为2,以及点D的坐标,即可确定出其他三点的坐标.(2)根据直线
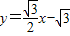 的解析式,易求得点P的坐标,而A、B的坐标在(1)题已经求得,即可利用待定系数法求出该抛物线的解析式.
的解析式,易求得点P的坐标,而A、B的坐标在(1)题已经求得,即可利用待定系数法求出该抛物线的解析式.(3)可用配方法将(2)题所得函数解析式化为顶点坐标式,进而可求出其顶点坐标,再根据坐标来判断它在△ABC中的特殊位置.
解答:
 解:(1)依题意,四边形ABDC为菱形,
解:(1)依题意,四边形ABDC为菱形,∵AB=2,∠CAB=60°,
∴C、D两点纵坐标均为
 ;
;设
 ,
,∵点D在直线
 上,
上,∴
 ,
,∴
 ;
;如图,(4分)
(2)
 ,抛物线过A、B、P三点,
,抛物线过A、B、P三点,∴

解得
 ;
;∴
 .(6分)
.(6分)(3)
 =
= ,
,∴顶点
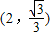 ;(7分)
;(7分)这个点在△ABC的内心位置.(8分)
(答外心、重心、垂心均可)
点评:此题主要考查了图形的旋转变换、等边三角形的性质、二次函数界限的确定等知识.正确的求出点D的坐标是解决此题的关键,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上.
上. 与y轴交于点P,抛物线y=ax2+bx+c,过A、B、P三点,求这条抛物线的函数关系式;
与y轴交于点P,抛物线y=ax2+bx+c,过A、B、P三点,求这条抛物线的函数关系式;

 的图象经过点(-1,3)
的图象经过点(-1,3)