Question

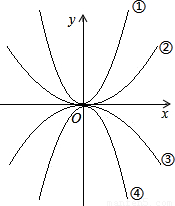
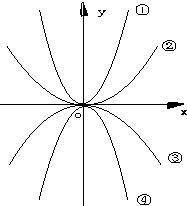8、如图，四个二次函数的图象中，分别对应的是：①y=ax²；②y=bx²；③y=cx²；④y=dx²，则a，b，c，d的大小关系是（　　）

A、a＞b＞c＞d

B、a＞b＞d＞c

C、b＞a＞c＞d

D、b＞a＞d＞c

Answer 1

分析：图中函数均以原点为顶点，y轴为对称轴，根据开口宽窄和方向解答．

解答：解：由二次函数y=ax²的性质知，
（1）抛物线y=ax²的开口大小由|a|决定．
|a|越大，抛物线的开口越窄；
|a|越小，抛物线的开口越宽．
（2）抛物线y=ax²的开口方向由a决定．
当a＞0时，开口向上，抛物线（除顶点外）都在x轴上方；
当a＜0时，开口向下，抛物线（除顶点外）都在x轴下方．
根据以上结论知：a＞b＞0，0＞c＞d．
故选A．

点评：此题只要熟悉二次函数的性质，就可以解答．