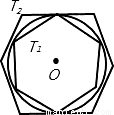
题目内容
如图,有一个圆O和两个正六边形T1,T2.T1的6个顶点都在圆周上,T2的6条边都和圆O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).若设T1,T2的边长分别为a,b,圆O的半径为r,则r:a=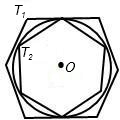 正六边形T1,T2的面积比S1:S2的值是
正六边形T1,T2的面积比S1:S2的值是分析:根据题意画出图形,连接OE、OG,OF,由正六边形T1,得到∠EOF为60°,从而得到△EOF为等边三角形,即a=r,故得到a:r=1:1;在Rt△EOG中,由OG为角平分线,得到∠EOG=30°,利用特殊角的三角函数可求出OE及OG的长,即为r:b的比值,然后求出a:b的比值,根据正六边形T1,T2相似,其面积之比等于边长之比的平方,即可求出面积之比.
解答: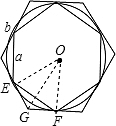 解:连接OE、OG,OF,
解:连接OE、OG,OF,
∵EF=a,且正六边形T1,
∴△OEF为等边三角形,OE为圆的半径r,
∴a:r=1:1;
由题意可知OG为∠FOE的平分线,即∠EOG=
∠EOF=30°,
在Rt△OEG中,OE=r,OG=b,
∵
=
=cos∠EOG=cos30°,即
=
,
∵r:a=1:1①;r:b=
:2②;
∴②:①得,a:b=
:2,且两个正六边形T1,T2相似,
∴S1:S2=a2:b2=3:4.
故答案为:r:a=1:1;r:b=
:2;S1:S2=3:4.
 解:连接OE、OG,OF,
解:连接OE、OG,OF,∵EF=a,且正六边形T1,
∴△OEF为等边三角形,OE为圆的半径r,
∴a:r=1:1;
由题意可知OG为∠FOE的平分线,即∠EOG=
| 1 |
| 2 |
在Rt△OEG中,OE=r,OG=b,
∵
| OE |
| OG |
| r | ||
|
| r |
| b |
| ||
| 2 |
∵r:a=1:1①;r:b=
| 3 |
∴②:①得,a:b=
| 3 |
∴S1:S2=a2:b2=3:4.
故答案为:r:a=1:1;r:b=
| 3 |
点评:本题考查的是正多边形和圆及特殊角的三角函数值,解答此题的关键是根据题意画出图形,再由三角函数的定义及特殊角的三角函数值求解.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
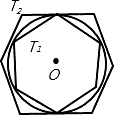 别为圆O的内接正六边形和外切正六边形).
别为圆O的内接正六边形和外切正六边形).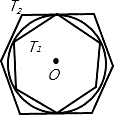 别为圆O的内接正六边形和外切正六边形).
别为圆O的内接正六边形和外切正六边形).