题目内容
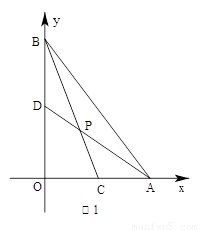
已知:点A、B分别在直角坐标系的x、y轴的正半轴上,O是坐标原点,点C在射线AO上,点D在线段OB上,直线AD与线段BC相交于点P,设 =a,
=a, =b,
=b, =k.
=k.(1)如图1,当a=
 ,b=1时,请求出k的值;
,b=1时,请求出k的值;(2)当a=
 ,b=1时(如图2),请求出k的值;当a=
,b=1时(如图2),请求出k的值;当a= ,b=
,b= 时,k=______;
时,k=______;(3)根据以上探索研究,请你解决以下问题:①请直接写出用含a,b代数式表示k=______;②若点A(8,0),点B(0,6),C(-2,0),直线AD为:y=-
 x+4,则k=______.
x+4,则k=______.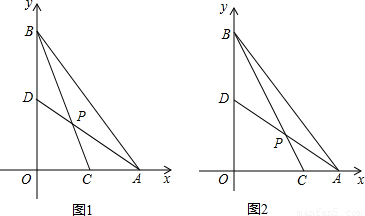
【答案】分析:(1)当a= ,b=1时,由条件可以得知设
,b=1时,由条件可以得知设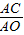 =
= ,
,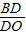 =1,可以得出D、C是OB、OA的中点,作DE∥OA交BC于点E,根据三角形的中位线定理和平行线分线段成比例定理可以得出结论.
=1,可以得出D、C是OB、OA的中点,作DE∥OA交BC于点E,根据三角形的中位线定理和平行线分线段成比例定理可以得出结论.
(2)如图2,作DF∥OA交BC于点F,根据三角形相似的性质和平行线分线段成比例定理可以同(1)一样的方法得出结论,如图3,作GB∥OC交PA于点G,可以得出△GBD∽△AD,△PGB∽△PAC.由相似三角形的性质及在a= ,b=
,b= 的情况下就可以得出结论.
的情况下就可以得出结论.
(3)①通过(1)、(2)的计算就可以得出:a= ,b=1时,k=
,b=1时,k=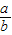 =
=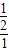 =
= ,a=
,a= ,b=1时,k=
,b=1时,k=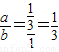 ,当a=
,当a= ,b=
,b= 时,k=
时,k=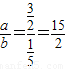 ,从而可以得出结论:k=
,从而可以得出结论:k=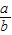 ;
;
②根据直线AD的解析式y=- x+4可以求出D点的坐标,从而求出OD的值,再由点A(8,0),点B(0,6),C(-2,0)就可以求出AO,CO,AC的值,从而可以求出a、b的值,直接运用k=
x+4可以求出D点的坐标,从而求出OD的值,再由点A(8,0),点B(0,6),C(-2,0)就可以求出AO,CO,AC的值,从而可以求出a、b的值,直接运用k=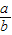 就可以求出结论.
就可以求出结论.
解答: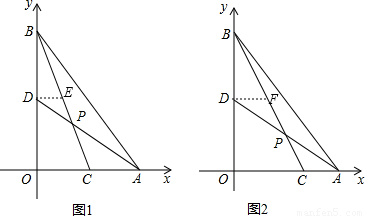 解:(1)如图1,作DE∥OA交BC于点E,
解:(1)如图1,作DE∥OA交BC于点E,
∵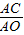 =a,
=a,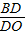 =b,且a=
=b,且a= ,b=1,
,b=1,
∴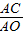 =
= ,
,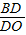 =1,
=1,
∴AO=2AC,BD=DO,
∴D、C是OB、OA的中点.
∴OC=AC.
∵DE∥OA,
∴BE=CE,
∴DE= OC,
OC,
∴DE= AC.
AC.
∵DE∥OA,
∴△DEP∽△ACP,
∴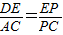 ,
,
∴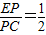 ,
,
∴PC=2PE,
∴EC=3PE,
∴BE=3PE,
∴BP=4PE.
∴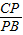 =
=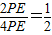 ,
,
∵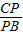 =k,
=k,
∴k= ;
;
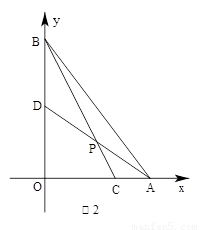
(2)如图2,作DF∥OA交BC于点F,
∵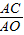 =a,
=a, =b,且a=
=b,且a= ,b=1,
,b=1,
∴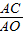 =
= ,
,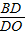 =1
=1
∴AO=3AC,BD=DO,
∴OC=2AC.
∵DF∥OA,
∴BF=CF,DF= OC,
OC,
∴DF=AC.
∵DF∥OA,
∴△DFP∽△ACP,
∴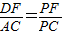 =1,
=1,
∴PF=PC,
∴CF=2PC,
∴BP=3PC,
∴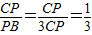 ,
,
∵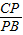 =k,
=k,
∴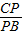 =
= ,
,
∴k= ;
;
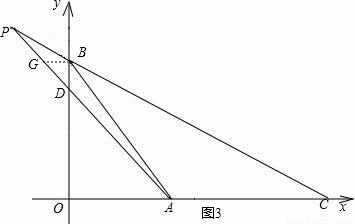 如图3,作GB∥OC交PA于点G,
如图3,作GB∥OC交PA于点G,
∴△GBD∽△AD,△PGB∽△PAC.
∴ ,
,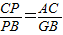 .
.
∵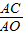 =a,
=a,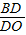 =b,
=b,
a= ,b=
,b= 时,
时,
∴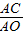 =
= ,
,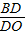 =
=
∴2AC=3AO,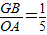 ,
,
∴AC= AO,AO=5GB,
AO,AO=5GB,
∴AC=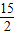 GB,
GB,
∴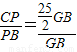 =
=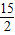 .
.
∵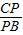 =k,
=k,
∴k=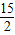 ;
;
(3)①通过(1)、(2)的计算就可以得出:
a= ,b=1时,k=
,b=1时,k=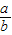 =
=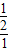 =
= ,
,
a= ,b=1时,k=
,b=1时,k=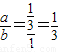 ,
,
a= ,b=
,b= 时,k=
时,k= ,
,
从而可以得出结论:k=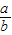 ;
;
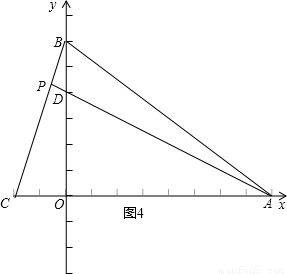 ②如图4,∵AD的解析式y=-
②如图4,∵AD的解析式y=- x+4,
x+4,
∴当x=0时,y=4,
∴D(0,4),
∴OD=4,
∵点A(8,0),点B(0,6),C(-2,0),
∴OA=8,OB=6,OC=2,
∴AC=10,BD=2.2
∵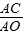 =a,
=a,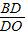 =b,
=b,
∴a=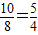 ,b=
,b=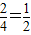 ,
,
∴k=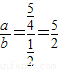
故答案为: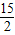 ,
,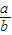 ,
, .
.
点评:本题是一道相似形综合试题,考查了作平行线在相似形中的运用,相似三角形的判定及性质的运用,由特殊到一般的数学思想的运用,解答是寻找k与a、b之间的关系式是关键.
 ,b=1时,由条件可以得知设
,b=1时,由条件可以得知设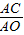 =
= ,
,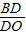 =1,可以得出D、C是OB、OA的中点,作DE∥OA交BC于点E,根据三角形的中位线定理和平行线分线段成比例定理可以得出结论.
=1,可以得出D、C是OB、OA的中点,作DE∥OA交BC于点E,根据三角形的中位线定理和平行线分线段成比例定理可以得出结论.(2)如图2,作DF∥OA交BC于点F,根据三角形相似的性质和平行线分线段成比例定理可以同(1)一样的方法得出结论,如图3,作GB∥OC交PA于点G,可以得出△GBD∽△AD,△PGB∽△PAC.由相似三角形的性质及在a=
 ,b=
,b= 的情况下就可以得出结论.
的情况下就可以得出结论.(3)①通过(1)、(2)的计算就可以得出:a=
 ,b=1时,k=
,b=1时,k=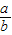 =
=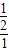 =
= ,a=
,a= ,b=1时,k=
,b=1时,k=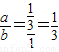 ,当a=
,当a= ,b=
,b= 时,k=
时,k=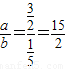 ,从而可以得出结论:k=
,从而可以得出结论:k=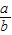 ;
;②根据直线AD的解析式y=-
 x+4可以求出D点的坐标,从而求出OD的值,再由点A(8,0),点B(0,6),C(-2,0)就可以求出AO,CO,AC的值,从而可以求出a、b的值,直接运用k=
x+4可以求出D点的坐标,从而求出OD的值,再由点A(8,0),点B(0,6),C(-2,0)就可以求出AO,CO,AC的值,从而可以求出a、b的值,直接运用k=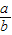 就可以求出结论.
就可以求出结论.解答:
 解:(1)如图1,作DE∥OA交BC于点E,
解:(1)如图1,作DE∥OA交BC于点E,∵
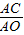 =a,
=a,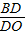 =b,且a=
=b,且a= ,b=1,
,b=1,∴
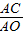 =
= ,
,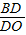 =1,
=1,∴AO=2AC,BD=DO,
∴D、C是OB、OA的中点.
∴OC=AC.
∵DE∥OA,
∴BE=CE,
∴DE=
 OC,
OC,∴DE=
 AC.
AC.∵DE∥OA,
∴△DEP∽△ACP,
∴
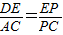 ,
,∴
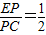 ,
,∴PC=2PE,
∴EC=3PE,
∴BE=3PE,
∴BP=4PE.
∴
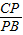 =
=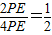 ,
,∵
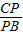 =k,
=k,∴k=
 ;
;(2)如图2,作DF∥OA交BC于点F,
∵
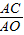 =a,
=a, =b,且a=
=b,且a= ,b=1,
,b=1,∴
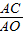 =
= ,
,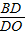 =1
=1∴AO=3AC,BD=DO,
∴OC=2AC.
∵DF∥OA,
∴BF=CF,DF=
 OC,
OC,∴DF=AC.
∵DF∥OA,
∴△DFP∽△ACP,
∴
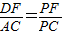 =1,
=1,∴PF=PC,
∴CF=2PC,
∴BP=3PC,
∴
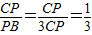 ,
,∵
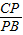 =k,
=k,∴
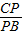 =
= ,
,∴k=
 ;
; 如图3,作GB∥OC交PA于点G,
如图3,作GB∥OC交PA于点G,∴△GBD∽△AD,△PGB∽△PAC.
∴
 ,
,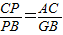 .
.∵
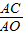 =a,
=a,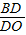 =b,
=b,a=
 ,b=
,b= 时,
时,∴
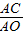 =
= ,
,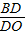 =
=
∴2AC=3AO,
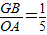 ,
,∴AC=
 AO,AO=5GB,
AO,AO=5GB,∴AC=
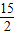 GB,
GB,∴
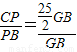 =
=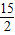 .
.∵
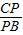 =k,
=k,∴k=
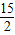 ;
;(3)①通过(1)、(2)的计算就可以得出:
a=
 ,b=1时,k=
,b=1时,k=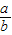 =
=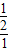 =
= ,
,a=
 ,b=1时,k=
,b=1时,k=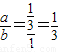 ,
,a=
 ,b=
,b= 时,k=
时,k= ,
,从而可以得出结论:k=
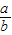 ;
; ②如图4,∵AD的解析式y=-
②如图4,∵AD的解析式y=- x+4,
x+4,∴当x=0时,y=4,
∴D(0,4),
∴OD=4,
∵点A(8,0),点B(0,6),C(-2,0),
∴OA=8,OB=6,OC=2,
∴AC=10,BD=2.2
∵
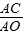 =a,
=a,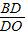 =b,
=b,∴a=
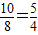 ,b=
,b=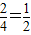 ,
,∴k=
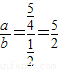
故答案为:
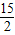 ,
,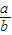 ,
, .
.点评:本题是一道相似形综合试题,考查了作平行线在相似形中的运用,相似三角形的判定及性质的运用,由特殊到一般的数学思想的运用,解答是寻找k与a、b之间的关系式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目