题目内容
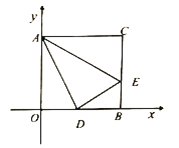
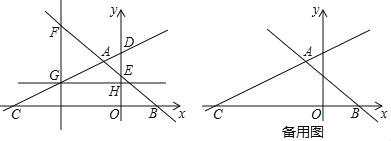
【题目】如图,在平面直角坐标系中,直线AB:y=﹣![]() x+
x+![]() 与直线AC:y=
与直线AC:y=![]() +8交于点A,直线AB分别交x轴、y轴于B、E,直线AC分别交x轴、y轴于点C、D.
+8交于点A,直线AB分别交x轴、y轴于B、E,直线AC分别交x轴、y轴于点C、D.
(1)求点A的坐标;
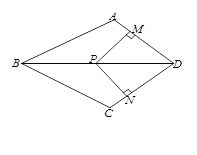
(2)在y轴左侧作直线FG∥y轴,分别交直线AB、直线AC于点F、G,当FG=3DE时,过点G作直线GH⊥y轴于点H,在直线GH上找一点P,使|PF﹣PO|的值最大,求出P点的坐标及|PF﹣PO|的最大值;
(3)将一个45°角的顶点Q放在x轴上,使其角的一边经过A点,另一边交直线AC于点R,当△AQR为等腰直角三角形时,请直接写出点R的坐标.
【答案】(1)(﹣2,7);(2)(![]() ,4),
,4),![]() ;(3)①(5,
;(3)①(5,![]() ),②(﹣9,
),②(﹣9,![]() )或(5,
)或(5,![]() )或(12,14)或(﹣
)或(12,14)或(﹣![]() ,
,![]() ).
).
【解析】
(1)联立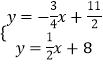 ,解得:
,解得:![]() ,故点A的坐标为(﹣2,7);
,故点A的坐标为(﹣2,7);
(2)当F、P、O三点共线时,|PF﹣PO|的值最大,即可求解;
(3)△AQR为等腰直角三角形,有如下图所示的两种情况,①AQ⊥AC,②当R'Q'⊥AC,分别求解即可.
(1)联立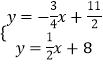 ,解得:
,解得:![]() ,故点A的坐标为(﹣2,7);
,故点A的坐标为(﹣2,7);
(2)由题意得:点E、D、B、C的坐标分别为(0,![]() )、(0,8)、(
)、(0,8)、(![]() ,0)、(﹣16,0).
,0)、(﹣16,0).
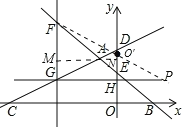
过点A作MN∥x轴,分别交FG、DE于点M、N,则:AN=2.
∵FG∥DE,
∴△AFG∽△AED,∴![]() 3,则AM=6,
3,则AM=6,
∴点M的横坐标为:﹣8,
则点F、G的坐标分别为(﹣8,![]() )、(﹣8,4),
)、(﹣8,4),
在y轴上找到点O关于直线GH的对称点O'(0,8),
连接FO'并延长,交直线GH于点P,此时,|PF﹣PO|的值最大,最大值为PO',
直线O'F的表达式为:y![]() x+8,
x+8,
当y=4时,x![]() ,即点P坐标为(
,即点P坐标为(![]() ,4),|PF﹣PO|=FO'
,4),|PF﹣PO|=FO'![]() ,故:点P坐标为(
,故:点P坐标为(![]() ,4),|PF﹣PO|
,4),|PF﹣PO|![]() ;
;
(3)△AQR为等腰直角三角形,有如下图所示的两种情况:
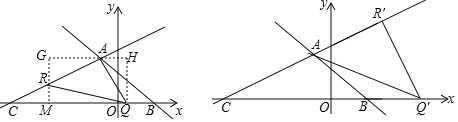
①当AQ⊥AC,当点R在点A下方时,
∴直线AQ的表达式为:y=﹣2x+b,将点A坐标代入得:7=﹣2×(﹣2)+b,解得:b=3,故:直线AQ的表达式为:y=﹣2x+3,则点Q坐标为(![]() ,0),过点A作x轴的平行线,过点R作y轴的平行线,过点Q作y轴的平行线,围成矩形GMQH,∠GAR+∠QAH=90°,∠QAH+∠AQH=90°,
,0),过点A作x轴的平行线,过点R作y轴的平行线,过点Q作y轴的平行线,围成矩形GMQH,∠GAR+∠QAH=90°,∠QAH+∠AQH=90°,
∴∠AQH=∠GAR,∠AGR=∠QHA=90°,AR=AQ,
∴△AGR≌△QHA(AAS),
∴HQ=GA=7,GR=AH=2![]() ,OM=2+GA=9,
,OM=2+GA=9,
∴RM=7![]() .
.
故点R的坐标为(﹣9,![]() ),当点R在点A上方时,同理可得点R坐标为(5,
),当点R在点A上方时,同理可得点R坐标为(5,![]() );
);
②当R'Q'⊥AC时,同理,点R'的坐标为(12,14)或(﹣16,0).
综上所述:点R的坐标为(﹣9,![]() )或(5,
)或(5,![]() )或(12,14)或(
)或(12,14)或(![]() ).
).

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案