��Ŀ����
����Ŀ������0��1�Լ������p��q��r����p<q<r�����dz�qΪp��r���м������Ϊ�˰����������м�������������±���

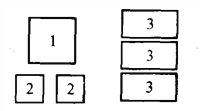
�������ȵ�����������������м���������磺�ϱ��е������е�3������![]() ��
��![]() ��
��![]() ����
����![]() ������
������![]() Ϊ
Ϊ![]() ��
��![]() ��һ���м�������ڱ��л������ҵ�
��һ���м�������ڱ��л������ҵ�![]() ��
��![]() ������
������![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ���������һֱд��ȥ�������ҵ�
���������һֱд��ȥ�������ҵ�![]() ��
��![]() �����������
�����������
��1�����ϱ������й��ɣ�����������գ�
���ϱ���������Ӧ�����Ϊ ��
�����������ı�һֱд��ȥ����ô���е�һ�����ֵ�![]() ��
��![]() �������� ��
�������� ��
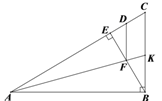
��2�������![]() ��
��![]() ��a��b��c��d����������
��a��b��c��d���������� ![]() ��
�� ![]() ����һ���м�������ú�a��b��c��d��ʽ�ӱ�ʾ������֤����
����һ���м�������ú�a��b��c��d��ʽ�ӱ�ʾ������֤����
��3����![]() ��
��![]() ��m��n��s�� t��������������
��m��n��s�� t��������������![]() ��
��![]() ����������
���м��������![]() ����СֵΪ ��
����СֵΪ ��
���𰸡���1����![]() ����
����![]() ��2��֤����������3��1504
��2��֤����������3��1504
�������������������1���ٹ۲�ÿһ�еĹ��ɿɵ�����λ�ڵڢ��У��������еĹ��ɿ�֪��![]() ��
��
�ڹ۲�����֪��һ�����ֵ�![]() ��
��![]() ���м�����ڵڢ��У���
���м�����ڵڢ��У���![]() ��
��
��2���𰸲�Ψһ�����ݱ����й۲쵽�ģ�����Ϊ![]() ��ͨ���Ƶ�֤�����ɵã�
��ͨ���Ƶ�֤�����ɵã�
��3���������п�֪![]() ��
��![]() ��������
��������![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �ȣ��ɴ˿ɵ�.
�ȣ��ɴ˿ɵ�.
�����������1���ٹ۲�ÿһ�еĹ��ɿɵ�����λ�ڵڢ��У������ӵ������֪��![]() ��
��
�ڹ۲�����֪��һ�����ֵ�![]() ��
��![]() ���м�����ڵڢ��У���
���м�����ڵڢ��У���![]() ��
��
�ʴ�Ϊ����![]() ����
����![]() ��
��
��2��������۲�Ψһ��֤����Ψһ���磺
���ۣ� ![]() ��
��
��a��b��c��d���������� ![]() ��
�� ![]() ��
��
��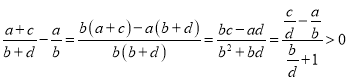 ��
��
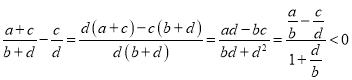 ��
��
��![]() ��
��
��3���������п�֪![]() ��
��![]() ��������
��������![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �ȣ��ɴ˿ɵ�mn����СֵΪ1504��
�ȣ��ɴ˿ɵ�mn����СֵΪ1504��
�ʴ�Ϊ��1504.

����Ŀ�������Ϊ�Ӽס��������˶�Ա��ѡ��һ�˲μӱ����������ǽ��������β��ԣ����Գɼ����±�����λ��������
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | ƽ���ɼ� | ��λ�� | |
�� | 10 | 8 | 9 | 8 | 10 | 9 | 9 | �� |
�� | 10 | 7 | 10 | 10 | 9 | 8 | �� | 9.5 |
��1����ɱ�����բ� ���� ��
��2�����������β��Գɼ��ķ��
��3���������β��Գɼ�����Ϊ![]() ������Ϊ�Ƽ�˭�μӱ��������ʣ���˵�����ɣ�
������Ϊ�Ƽ�˭�μӱ��������ʣ���˵�����ɣ�