题目内容
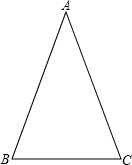
已知A、B为直角三角形ABC的两锐角,那么方程(cotA)x2-2x+cotB=0
- A.有两个不相等的实根
- B.有两个相等的实根
- C.没有实根
- D.根的情况不能确定
B
分析:根据根的判别式△=b2-4ac的符号判断方程(cotA)x2-2x+cotB=0的根的情况.
解答:∵方程(cotA)x2-2x+cotB=0的二次项系数a=cotA,一次项系数b=-2,常数项c=cotB,
∴△=b2-4ac=4-4cotAcotB;
又∵A、B为直角三角形ABC的两锐角,
∴cotA=tanB,
∴△=4-4tanBcotB=4-4=0,即△=0,
∴原方程有两个相等的实数根.
故选B.
点评:本题考查了根的判别式、锐角三角函数的定义.解答该题时,根据锐角三角函数的定义求得cotA=tanB是求根的判别式的符号的关键.
分析:根据根的判别式△=b2-4ac的符号判断方程(cotA)x2-2x+cotB=0的根的情况.
解答:∵方程(cotA)x2-2x+cotB=0的二次项系数a=cotA,一次项系数b=-2,常数项c=cotB,
∴△=b2-4ac=4-4cotAcotB;
又∵A、B为直角三角形ABC的两锐角,
∴cotA=tanB,
∴△=4-4tanBcotB=4-4=0,即△=0,
∴原方程有两个相等的实数根.
故选B.
点评:本题考查了根的判别式、锐角三角函数的定义.解答该题时,根据锐角三角函数的定义求得cotA=tanB是求根的判别式的符号的关键.

练习册系列答案
相关题目
 互唯一确定的.
互唯一确定的.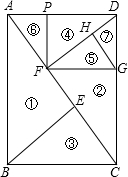 知线段AB=1,∠BAC=θ.
知线段AB=1,∠BAC=θ.
