题目内容
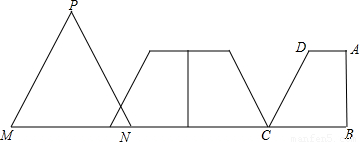
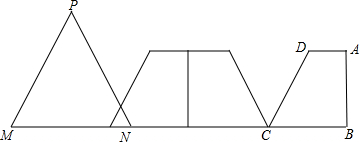
习题改编.原题:梯形ABCD,AD∥BC,∠B=90°,∠DCB=60°,BC=4,AD=2,△PMN,PM=MN=NP=a,BC与MN在一直线上,NC=6,将梯形ABCD向左翻折180°.
(1)向左翻折二次,a≥2时,求两图形重叠部分的面积;
(2)向左翻折三次,重叠部分的面积等于梯形ABCD的面积,a的值至少应为多少?
(3)向左翻折三次,重叠部分的面积恰好等于梯形ABCD的面积的一半,求a的值.
分析:(1)因为∠DCB=60°,△PMN也是等边三角形,这样容易知道△EGN也是等边三角形,易求GN=2,所以求两图形重叠部分的面积就可以求出;
(2)如图,等边三角形的边长MN=GN+HG+MH,其中只要求MH,利用已知解Rt△KHM就可以了;
(3)若现在重叠部分的面积等于直角梯形ABCD的面积的一半,如图首先判断HG的大小,梯形ABCD的面积可以直接求出;然后设HG为x,根据已知条件可以得到关于x的方程,解方程就可以得到题目的结果.
(2)如图,等边三角形的边长MN=GN+HG+MH,其中只要求MH,利用已知解Rt△KHM就可以了;
(3)若现在重叠部分的面积等于直角梯形ABCD的面积的一半,如图首先判断HG的大小,梯形ABCD的面积可以直接求出;然后设HG为x,根据已知条件可以得到关于x的方程,解方程就可以得到题目的结果.
解答:解:(1)∵CB=4,CN=6,∴GN=2.
又∵∠PNM=60°且∠EGN=60°,
∴△EGN为正三角形.
∴△EGN的高为h=
.
∴S△EGN=
×2×
=
;
(2)在直角梯形ABCD中,
∵CD=4,∠DCB=60°,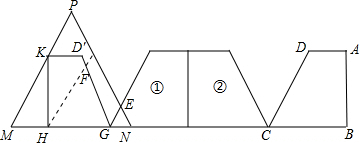
∴AB=2
.
在Rt△KHM中,tan30°=
,
MH=2
×
=2,
∴MN=2+4+2=8;
(3)S梯形ABCD=
(2+4)•2
=6
.
当MP经过H点时,交D′G于F,
则 S△HGF=
×4×2
=4
>
S梯形ABCD.
∴HG<4,
设HG=x,则有 h′=
x.
∴S公共部分=
x•
x=
x2.
∴
x2=3
,
解得:x=2
或-2
(舍去).
∵GN=2,
∴等边三角形PNM的边长a为(2
+2)cm.
又∵∠PNM=60°且∠EGN=60°,
∴△EGN为正三角形.
∴△EGN的高为h=
| 3 |
∴S△EGN=
| 1 |
| 2 |
| 3 |
| 3 |
(2)在直角梯形ABCD中,
∵CD=4,∠DCB=60°,

∴AB=2
| 3 |
在Rt△KHM中,tan30°=
| MH |
| KH |
MH=2
| 3 |
| ||
| 3 |
∴MN=2+4+2=8;
(3)S梯形ABCD=
| 1 |
| 2 |
| 3 |
| 3 |
当MP经过H点时,交D′G于F,
则 S△HGF=
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
∴HG<4,
设HG=x,则有 h′=
| ||
| 2 |
∴S公共部分=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
∴
| ||
| 4 |
| 3 |
解得:x=2
| 3 |
| 3 |
∵GN=2,
∴等边三角形PNM的边长a为(2
| 3 |
点评:本题考查了翻折变换及直角梯形的知识,难度较大,图形变换比较复杂,考查了等边三角形的性质,面积计算,也考查了解直角三角形的知识,综合性比较强,注意后面两问表述的重叠面积的大小.

练习册系列答案
相关题目