题目内容
小聪、小明、小伶、小俐四人共同探究代数式2x2-4x+6的值的情况.他们作了如下分工:小聪负责找值为0时x的值,小明负责找值为4时x的值,小伶负责找最小值,小俐负责找最大值.几分钟后,各自通报探究的结论,其中错误的是
- A.小聪认为找不到实数x,使2x2-4x+6的值为0
- B.小明认为只有当x=1时,2x2-4x+6的值为4
- C.小伶发现2x2-4x+6的值随x的变化而变化,因此认为没有最小值
- D.小俐发现当x取大于2的实数时,2x2-4x+6的值随x的增大而增大,因此认为没有最大值
C
分析:设y=2x2-4x+6,根据二次函数的顶点坐标,可求得最小值,再分别代入y=0和y=4时的x的值,从而得出答案.
解答:设y=2x2-4x+6,
配方得,y=2(x2-2x)+6=2(x2-2x+1)+6-2=2(x-1)2+4,
函数有最小值4,此时x=1;
当y=0时,x不存在;
当y=4时,x=1;
函数不存在最大值.
故选C.
点评:本题考查了二次函数的最值问题,以及已知函数值求自变量的值,是基础知识要熟练掌握.
分析:设y=2x2-4x+6,根据二次函数的顶点坐标,可求得最小值,再分别代入y=0和y=4时的x的值,从而得出答案.
解答:设y=2x2-4x+6,
配方得,y=2(x2-2x)+6=2(x2-2x+1)+6-2=2(x-1)2+4,
函数有最小值4,此时x=1;
当y=0时,x不存在;
当y=4时,x=1;
函数不存在最大值.
故选C.
点评:本题考查了二次函数的最值问题,以及已知函数值求自变量的值,是基础知识要熟练掌握.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
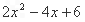 的值的情况.他们作了如下分工:小聪负责找值为0时x的值,小明负责找值为4时x的值,小伶负责找最小值,小俐负责找最大值.几分钟后,各自通报探究的结论,其中错误的是
的值的情况.他们作了如下分工:小聪负责找值为0时x的值,小明负责找值为4时x的值,小伶负责找最小值,小俐负责找最大值.几分钟后,各自通报探究的结论,其中错误的是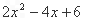 的值为0
的值为0 的值为4
的值为4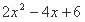 的值随
的值随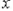 的变化而变化,因此认为没有最小值
的变化而变化,因此认为没有最小值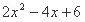 的值随x的增大而增大,因此认为没有最大值
的值随x的增大而增大,因此认为没有最大值