题目内容
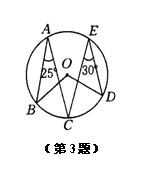
如图，∠AOB＝100°，OF是∠BOC的平分线，∠AOE＝∠EOD，∠EOF＝140°，求：∠COD的度数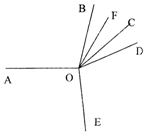
∠COD＝20°
分析：设∠COD=x，∠BOC+∠AOD=y，由OF平分∠BOC，∠AOE=∠DOE，可得x+1/2y=140°，图中六个角之和为360°，可得x+y+100°=360°，联立方程组解得x．
解：设∠COD=x，∠BOC+∠AOD=y，
∵OF平分∠BOC，∠AOE=∠DOE
∴x+1/2y=140°①，
∵六个角之和为360°，
∴x+y+100°=360°②，
联立①②解得：x=20°，
∴∠COD的度数为20°．
故答案为：20°
练习册系列答案
相关题目
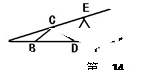
上有若干个点
、
、…、
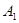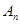，每相邻两点之间的距离都为1，点
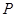是线段
上的一个动点．
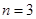时，则点
的距离之和的最小值是______；
时，则当点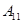
的距离之和有最小值，且最小值是_________ ． 
、
被
、
所截，且
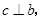
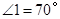，则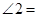
_________
.
